Rumus Volume Bangkit Ruang Lengkap + Pola Soal

Rumus Volume Bangun Ruang

Seperti pembahasan sebelumnya, bangkit ruang yaitu bangkit Matematika yang mempunyai isi atau volume. Selain mempunyai volume, bangkit ruang juga mempunyai luas permukaan. Dan berikut ini yaitu rumus volume bangkit ruang yang mencakup balok, kubus, prisma tegak segitiga, limas segi tiga, limas segi empat, tabung, kerucut, dan bola.

Setelah mempelajari macam-macam bangkit ruang dan sifat-sifatnya, tentunya kita juga ingin mempelajari cara menghitung volume nya. Dan berikut ini yaitu rumus volume bangkit ruang lengkap disertai dengan rujukan soal dan jawabannya.

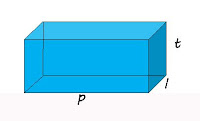
Balok

Volume Balok = Luas bantalan x tinggi 
Volume Balok = p x l x t

Contoh Soal
Diketahui panjang balok= 14 cm , lebar= 10 cm, tinggi= 8 cm. Hitunglah volume nya !

V = p x l x t
    =14 cm x 10 cm x 8 cm
    = 1.120 cm ³

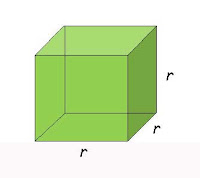
Kubus

Volume Kubus = rusuk x rusuk x rusuk (R³)
Rusuk disebut juga sisi (s)

Contoh soal
Diketahui rusuk kubus 8 cm. Hitunglah volume nya !

V = rusuk x rusuk x rusuk
   = 8 cm x 8 cm x 8 cm
   = 512 cm³

Prisma Tegak Segitiga

Volume Prisma Tegak Segitiga = Luas bantalan x tinggi
Volume Prisma Tegak Segitiga = (1/2 x a x tinggi segitiga) x tinggi prisma

Contoh soal
Diketahui sebuah prisma alasnya berbentuk segitiga siku-siku dengan panjang sisi 6 cm dan 8 cm. Tinggi prisma 12 cm. Hitunglah volume nya !

V = (1/2 x a x tinggi segitiga) x tinggi prisma
  = (1/2 x 6 cm x 8 cm) x 12 cm
  = 288 cm³

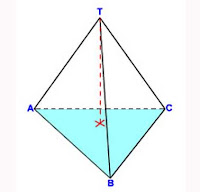
Limas Segitiga

Volume Limas Segitiga = 1/3 x luas bantalan x tinggi
Volume Limas Segitiga = 1/3 x (1/2 x a x t.segitiga) x t.limas

Contoh soal
Berdasarkan gambar. Diketahui sebuah limas mempunyai bantalan berbentuk segitiga siku-siku ABC dengan panjang sisinya 6 cm dan lebar 8 cm. Tinggi limas 15 cm. Hitunglah volume nya !

V = 1/3 x luas bantalan x tinggi
  = 1/3 x ( 1/2 x 6 x 8) x 15
  =  1/3 x 24 x 15
 = 120 cm³

Limas Segi Empat

Volume limas segi empat = 1/3 x luas bantalan x tinggi
Volume limas segi empat = 1/3 x (p x l) x tinggi limas

Contoh soal
Sebuah limas T.ABCD mempunyai bantalan berbentuk persegi panjang dengan panjang AB=CD= 10 cm dan panjang AD=BC= 8 cm. Jika tinggi limas tersebut yaitu 12 cm, tentukan volume limas tersebut !

V = 1/3 x (p x l) x tinggi limas
   = 1/3 x (10 cm x 8 cm) x 12 cm
  = 320 cm³

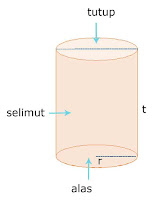
Tabung

Volume tabung = luas bantalan x tinggi
Volume tabung = π x r² x t
π  (phi) = 22/7 atau 3,14
r = jari-jari bantalan tabung
t = tinggi tabung
d = diameter/ garis tengah = 2 x r

Contoh soal
Diketahui diameter bantalan tabung 28 cm, tinggi tabung 35 cm. Hitunglah volumenya !

Diameter bantalan tabung = 28 cm. Berarti jari-jari (r) = 28 : 2 = 14 cm
V = π x r² x t
   = 22/7 x 14 cm x 14 cm x 35 cm
  = 21.560 cm³

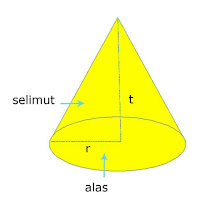
Kerucut

Volume kerucut = 1/3 x luas bantalan x tinggi kerucut
Volume Kerucut = 1/3 x π x r² x t

Contoh soal
Sebuah benda berbentuk kerucut mempunyai jari-jari 21 cm dan tingginya 35 cm. Hitunglah volumenya !

V = 1/3 x π x r² x t
  = 1/3 x 22/7 x 21 cm x 21 cm x 35 cm
  = 16.170 cm³

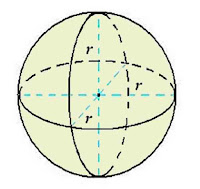
Bola

Volume Bola = 4/3 x  π x r³

Contoh soal
Sebuah bola plastik mempunyai diameter 21 cm. Hitunglah volume udara pada bola plastik tersebut !

Diameter bola 21 cm. Berarti jari-jarinya 10,5 cm
V = 4/3 x  π x r³
   = 4/3 x 22/7 x 10,5 cm x 10,5 cm x 10,5 cm
  = 4.851 cm³

Demikianlah pembahasan wacana Rumus Volume Bangun Ruang Lengkap + Contoh Soal yang dapat aku bagikan. Semoga bermanfaat.

Dan berikut ini yaitu Kumpulan Soal Bangun Ruang Lengkap plus Kunci Jawaban disertai file download yang dapat dipakai untuk latihan di rumah.