Pintar Pelajaran Persamaan Garis Singgung Lingkaran, Melalui Suatu Titik Di Dalam Dan Luar Lingkaran, Gradien, Teladan Soal, Pembahasan, Matematika

Persamaan Garis Singgung Lingkaran, Melalui Suatu Titik di Dalam dan Luar Lingkaran, Gradien, Contoh Soal, Pembahasan, Matematika - Berikut ini ialah bahan lengkapnya : (Baca juga : Persamaan Lingkaran)

1. Persamaan Garis Singgung Melalui Suatu Titik pada Lingkaran

Titik P(x₁, y₁) terletak pada garis g dan lingkaran x² + y² = r², seperti diperlihatkan pada Gambar 1. 

Gambar 1. Garis Singgung Melalui Suatu Titik pada Lingkaran.

Gradien garis yang menghubungkan titik O dan titik P adalah m_OP =  . Garis g menyinggung bundar di P, jelas OP ┴ g sehingga m_OP·m_g = –1 atau m_g =  . Akibatnya, gradien garis g ialah :

Jadi, persamaan garis singgung g ialah :

y – y₁ = mg(x – x₁) ↔ y – y₁ = x₁/y₁ (x – x₁)

↔ y₁(y – y₁) = –x₁(x – x₁)

↔ x₁x + y₁y = x₁² + y₁² .... (i)

Titik P(x₁, y₁) terletak pada lingkaran x² + y² = r²

sehingga :

x₁² + y₁² = r² ....(ii)

Apabila persamaan (ii) disubstitusikan ke persamaan (i) diperoleh :

g: x₁x + y₁y = r²

Persamaan tersebut ialah persamaan garis singgung yang melalui titik P(x₁, y₁) dan terletak pada bundar :

L : x² + y² = r²

Anda pun sanggup memilih persamaan garis singung g melalui titik P (x₁, y₁) yang terletak pada lingkaran

L : (x – a)² + (y – b) = r² dengan sentra di M(a, b) dan jari-jari r, yaitu :

g: (x – a) (x₁ – a) + (y – b) (y₁ – b) = r²

Bersama sobat sebangku, buktikan persamaan tersebut. Kemudian, kemukakan akibatnya di depan kelas (beberapa orang saja).

Diketahui titik P(x₁, y₁) terletak pada garis g dan bundar L: x² + y² + Ax + By + C = 0 menyerupai diperlihatkan pada Gambar 2. 

Gambar 2. Titik P(x₁, y₁) terletak pada garis g dan bundar L: x² + y² + Ax + By + C = 0.

Gradien garis yang menghubungkan titik T dan titik P ialah :

Garis g menyinggung bundar maka :

g ┴ TP dan m_g. m_MP = –1 sehingga :

Jadi, persamaan garis singgung g ialah :

y – y₁ = m_g (x – x₁)

y – y₁ =  (x – x₁)

(y – y₁) (y₁ – b) = – (x₁ – a) (x – x₁)

y₁y – by – y₁² + y₁b = –x₁x + x₁² + ax – ax₁

y₁y – by + y₁b + x₁x – ax + ax₁ = x₁² + y₁² .... (1)

Titik P(x₁, y₁) terletak pada bundar L sehingga diperoleh :

x₁² + y₁² + Ax₁ + By₁ + C = 0

x₁² + y₁² = – (Ax₁ + By₁ + C) .... (2)

Substitusikan (2) pada (1), diperoleh :

y₁y – by + y₁b + x₁x – ax + ax₁ = – (Ax₁ + By₁ + C) .... (3)

Dari uraian sebelumnya, diperoleh : -1/2 A = a, -1/2 B = b, .... (4)

Substitusikan (4) pada (3) sehingga persamaan (3) menjadi :

y₁y + ½ B y – ½ B y₁ + x₁x + ½ Ax – ½ A x₁ = – Ax₁ – By₁ – C

y₁y + ½ B y + ½ y₁ + x₁x + ½ A x + ½ A x₁ + C = 0

x₁x + y₁y + ½ A (x + x₁) + ½ B (y + y₁) + C = 0

Jadi, persamaan garis singgung yang melalui titik P(x₁, y₁) dan terletak pada bundar L: x² + y² + Ax + By + C = 0 ialah :

xx₁ + yy₁ + ½ A (x + x₁) + ½ B (y + y₁) + C = 0

Contoh Soal 1

Tentukan persamaan garis singgung pada lingkaran x² + y² = 25 di titik (4, –3).

Penyelesaian 1

Titik (4, –3) terletak pada bundar sebab 4² + (–3)² = 25. Persamaan garis singgung g: x₁x + y₁y = r² dengan x₁ = 4 dan y₁ = –3 ialah 4x – 3y = 25.

Contoh Soal 2

Tentukan persamaan garis singgung pada lingkaran (x + 2)² + (y – 1)² = 25 di titik (–6, 4).

Pembahasan 2

Titik (–6, 4) terletak pada bundar karena (–6 + 2)² + (4 – 1)² = 25. Diketahui a = –2 dan b = 1 maka persamaan garis singgung :

(x₁ – a)(x – a) + (y₁ – b)(y – b) = r²

(x₁ + 2)(x + 2) + (y₁ – 1) (y – 1) = 25

Untuk x₁ = –6 dan y₁ = 4 diperoleh :

(–6 + 2) (x + 2) + (4 – 1) (y – 1) = 25

–4 (x + 2) + 3(y – 1) = 25

–4x – 8 + 3y – 3 = 25

–4x + 3y = 14

2. Persamaan Garis Singgung Melalui Suatu Titik di Luar Lingkaran

Diketahui titik P(x₁, y₁) berada di luar bundar :

L: x² + y² = r² … (1)

Misalkan, persamaan garis singgung yang melalui :

P(x₁, y₁) ialah :

g: y = y₁ + m(x – x₁) …(2).

Jika g menyinggung L di titik Q, Anda sanggup menyubstitusikan persamaan (2) ke persamaan (1) sehingga diperoleh persamaan kuadrat dalam x. Selanjutnya, Anda cari diskriminan (D) persamaan kuadrat tersebut. Oleh lantaran g menyinggung L maka D = 0 sehingga nilai-nilai m sanggup diperoleh. Apabila nilai mdiketahui, Anda sanggup memilih persamaan garis singgung g dengan cara menyubstitusikan m ke persamaan garis g tersebut. Untuk lebih jelasnya, pelajari teladan berikut.

Contoh Soal 3

a. Carilah persamaan garis singgung pada lingkaran x² + y² = 25 yang sanggup ditarik dari titik (7, –1).

b. Tentukan koordinat-koordinat titik singgung.

c. Tentukan persamaan garis yang menghubungkan titik-titik singgung.

Jawaban 3

a. Titik P (7, –1) terletak di luar lingkaran. Coba Anda buktikan hal ini.

Misalkan, persamaan garis singgung yang melalui (7, –1) dengan gradien m ialah :

y + 1 = m(x – 7)

↔ y = mx – 7m – 1 ... (1)

Substitusi (1) ke persamaan lingkaran x² + y² = 25, diperoleh :

x² + (mx – 7m – 1)² = 25

x² + m²x² – 14m²x – 2mx + 49m² + 14m + 1 = 25

(1 + m²)x² – (14m² + 2m)x + (49m² + 14m – 24) = 0

Nilai diskriminan, yaitu :

D = (14m² + 2m)² – 4 (1 + m²) (49m² + 14m – 24)

D = 196m⁴ + 56m³ + 4m² – 100m² – 56m + 96 – 196m⁴ – 56m³

D = –96m² – 56m + 96

Syarat garis menyinggung bundar ialah D = 0 sehingga :

D = b² − 4.a.c = 0

⇔ (−2m² + 14m)² − 4(m² + 1)(m² − 14m + 24) = 0

⇔ 4m⁴ − 56m³ + 196m² − 4m⁴ + 56m³ − 96m² − 4m² + 56m − 96 = 0

⇔ 196m² − 96m² − 4m² − 56m − 96 = 0

⇔ 96m² + 56m − 96 = 0

⇔ 12m² + 7m − 12 = 0

(3m + 4)(4m − 3) = 0

m = 3/− 4 atau m = 4/3

Untuk m = 3/− 4 , maka persamaan garis singungnya ialah 4x + 3y − 25 = 0

Untuk m = 4/ 3 , maka persamaan garis singungnya ialah 3x − 4y + 25 = 0

b. Misalkan, titik A ialah titik singgung garis l: 4y – 3x + 25 = 0 dengan lingkaran.

l: 4y – 3x x + 25 = 0 atau l: y = 3/4 x - 25/4

Substitusi garis l ke persamaan lingkaran x² + y² = 25 diperoleh :

x² + (3/4 x - 25/3) 25 ⇔ x² + 9/16 x² - 75/8 x + 625/16 = 25

⇔ 25/16 x² - 75/8 x + 625/16 = 25

⇔ 25x² – 150x + 225 = 0

⇔ x² – 6x + 9 = 0

⇔ (x – 3)² = 0

⇔ x = 3.

Coba Anda substitusikan x = 3 pada persamaan garis singgung y = 3/4x - 25/4

Apakah Anda memperoleh titik singgung A (3, –4)?

Misalkan, titik B ialah titik singgung garis g: 3y + 4x – 25 = 0 dengan bundar :

g: 3y + 4x – 25 = 0 atau g: y = -4/3 x + 25/3

Substitusi garis g ke persamaan lingkaran x² + y² = 25 diperoleh :

x² + (4/3 x + 25/3) = 25 ⇔ x² + 16/9 x² - 200/9 x + 625/9 = 25

⇔ 25/9 x² - 200/9 x + 625/9 = 25

⇔ 25x² – 200x + 400 = 0

⇔ x² – 8x + 16 = 0

⇔ (x – 4)² = 0

⇔ x = 4

Coba Anda substitusikan x = 4 pada persamaan garis singgung  :

Apakah Anda memperoleh titik singgung B(4, 3)?

Jadi, koordinat titik singgung ialah A(–3, 4) dan B(4, 3).

c. Persamaan garis yang melalui titik A(–3, 4) dan B(4, 3) diperoleh dengan memakai rumus persamaan garis :

7y – 28 = –x – 3

x + 7y = 25

Persamaan garis yang menghubungkan titik singgung A dan B ialah x + 7y = 25.

Contoh Soal 4 : Soal Ebtanas 1998

Persamaan garis singgung melalui titik (9, 0) pada lingkaran x² + y² = 36 ialah :

Jawaban 4

Misalkan, persamaan garis singgung

y – 0 = m(x – 9)

y = mx – 9m

maka L

x² + (mx – 9)² = 36

x² + m²x² – 18mx + 81 = 36

(1 + m²)x² – 18mx + 45 = 0

syarat menyinggung:

(18m)² – 4(1 +m²)(45) = 0

324m² – 180m² – 180 = 0

144m² = 180

3. Persamaan Garis Singgung dengan Gradien Tertentu

Diketahui, persamaan garis dengan gradien m ialah g: y = mx + n. Jika titik Pterletak pada g dan lingkaran x² + y² = r² maka,

x² + (mx + n)² = r² ⇔ x² + m²x² + 2mnx + n² – r² = 0

⇔ (m² + 1)x² + 2mnx + (n² – r²) = 0

Syarat nilai diskriminan ialah D = 0 lantaran garis y = mx + n menyinggung lingkaran. Dengan demikian, (2mn)² – 4(m² + 1) (n² – r²) = 0

⇔ 4m²n² – 4m²n² + 4m²r² – 4n² + 4r² = 0

⇔ 4m²r² – 4n2 + 4r² = 0

⇔ 4n² = 4m²r² + 4r²

⇔ n² = (m2 + 1)r²

 atau 

Substitusikan nilai n ke persamaan garis y = mx + n, diperoleh : 

Persamaan garis singgung bundar L: x² + y² = r² dengan gradien m ialah :

Anda pun sanggup memilih persamaan garis singgung lingkaran L: (x – a)² + (y – b)² = r² untuk gradien m dengan titik sentra bundar T(a, b) dan jari-jari r, yaitu :

Bersama sobat sebangku, buktikan persamaan tersebut, akibatnya tuliskan dan jelaskan di depan kelas (beberapa siswa saja).

Contoh Soal 5

Carilah persamaan garis singgung pada lingkaran x² + y² = 4 dengan gradien m = –1.

Kunci Jawaban 5

Persamaan garis untuk gradien m = –1 ialah y = (–1) x + n atau y = –x + n. Substitusi persamaan garis ini ke persamaan lingkaran, diperoleh :

x² + (–x + n)² = 4 ⇔ x² + x² – 2nx + n² = 4

2x² – 2nx + (n² – 4) = 0

Nilai diskriminan untuk D = 0 adalah

D = 4n² – 8(n² – 4)

0 = –4n² + 32

n² = 8

 atau 

Jadi, persamaan garis singgung bundar adalah  dan 

Contoh Soal 6

Carilah persamaan garis singgung pada lingkaran (x – 2)² + (y – 3)² = 8 dengan gradien m = –1.

Penyelesaian 6

Persamaan lingkaran (x – 2)² + (y – 3)² = 8 mempunyai jari-jari . Persamaan garis singgung pada bundar tersebut ialah :

y – b = m (x – a) ± 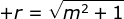 ⇔ y – 3 = (–1)(x – 2) ± 

⇔ y – 3 = –x + 2 ± 4

⇔ y = –x + 5 ± 4

Jadi, persamaan garis singgungnya ialah :

g₁: y = –x + 9 dan

g₂: y = –x + 1.

Contoh Soal 7

Garis g menghubungkan titik A(5, 0) dan titik B(10 cos θ, 10 sin θ). Titik P terletak pada AB sehingga AP : PB = 2 : 3. Jika θ berubah dari 0 hingga 2π maka titik P bergerak menelusuri suatu lingkaran. Tentukan persamaan bundar tersebut.

Pembahasan 7

Langkah ke-1

Menuliskan apa yang diketahui dan apa yang ditanyakan soal.

Diketahui : • garis g menghubungkan A(5, 0) dan B(10 cos θ, 10 sin θ)

• AP : PB = 2 : 3

Ditanyakan : Persamaan kurva.

Langkah ke-2

Menentukan konsep yang akan dipakai dalam menjawab soal. Pada soal ini, konsep yang dipakai ialah konsep perbandingan, konsep trigonometri, dan konsep persamaan umum lingkaran.

Langkah ke-3

Menentukan persamaan bundar dengan seni administrasi yang telah diketahui.

A(5, 0) dan B(10 cos θ, 10 sin θ). Titik P pada AB sehingga AP : PB = 3 : 2

Amati gambar berikut.

OP = OA + 2/5 AB

OP = OA + 2/5 (OB – OA)

OP = 3/5 OA + 2/5 OB

Persamaan parameter titik P ialah :

x = 3/5 . 5 + 2/5 . 10 cos θ = 3 + 4 cos θ:

y = 3/5 . 0 + 2/5 . 10 cos θ = 4 sin θ.

Dengan demikian, x = 3 + 4 cos θ  4 cos θ = x – 3

y = 4 sin θ  4 sin θ = y

(4 cos θ)²+ (4 sin θ)² = (x – 3)² +  y²

16 (cos² θ + sin² θ ) = x² – 6x + 9 + y²

x2 + y2 – 6x = 7

Jadi, persamaan lingkarannya ialah x² + y² – 6x = 7.

Anda kini sudah mengetahui Garis Singgung Lingkaran. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi :

Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.