Contoh Soal Rumus Persamaan Lingkaran, Pengertian Umum, Pusat O T M, Jari jari r, Posisi Titik dan Garis, Pembahasan, Jawaban, Matematika - Pada penggalan ini, konsep bundar akan dikembangkan pada bentuk umum persamaan bundar dan persamaan garis singgung lingkaran. Konsep bundar sangat penting peranannya dalam ilmu pengetahuan dan teknologi untuk memecahkan suatu persoalan menyerupai berikut.
 |
| Gambar 1. Gedung Parthenon. (Foto : Flickr via Wikimedia Commons [1] |
Gedung Parthenon dibangun 440 SM. Gedung tersebut dirancang oleh arsitek Yunani dengan memakai perbandingan nisbah emas. Amati gambar berikut.
Pada titik tengah sisi persegi ABCD dibentuk busur bundar dengan sentra G dan jari-jari  . Lingkaran tersebut memotong perpanjangan
. Lingkaran tersebut memotong perpanjangan  di F. Nisbah BF : AB disebut perbandingan nisbah emas. Menurut para ahli, perbandingan nisbah emas merupakan perbandingan yang paling yummy dipandang. Jika busur DF memenuhi persamaan x2 + y2 – 138y – 44 = 0, berapa perbandingan nisbah emas gedung Parthenon?
di F. Nisbah BF : AB disebut perbandingan nisbah emas. Menurut para ahli, perbandingan nisbah emas merupakan perbandingan yang paling yummy dipandang. Jika busur DF memenuhi persamaan x2 + y2 – 138y – 44 = 0, berapa perbandingan nisbah emas gedung Parthenon?
1. Persamaan Lingkaran
Gambar 2. memperlihatkan irisan kerucut berbentuk lingkaran. Pada gambar itu tampak bahwa bidang datarnya mengiris seluruh penggalan dari selimut dan tegak lurus sumbu kerucut.
 |
| Gambar 2. Irisan kerucut berbentuk lingkaran. |
Tentunya, Anda masih ingat definisi bundar yang telah dipelajari di SMP. Agar Anda ingat kembali, berikut ini disajikan definisi lingkaran.
Pengertian Lingkaran :
Lingkaran ialah daerah kedudukan titik-titik yang memiliki jarak yang sama terhadap satu titik tertentu.
1.1. Persamaan Lingkaran Berpusat di O (0, 0) dan Berjari-jari r
Amati Gambar 3.
Diketahui, titik P(x, y) ialah titik sebarang pada bundar L. Apabila titik P diproyeksikan pada sumbu-x maka diperoleh titik P' sehingga segitiga OPP' ialah segitiga siku-siku di P'.
 |
| Gambar 3. Lingkaran Berpusat di O (0, 0) dan Berjari-jari r. |
Pada segitiga OPP' berlaku Teorema Pythagoras sebagai berikut.
OP2 = (OP')2 + (P'P)2
↔ r2 = x2 + y2 Lingkaran L sanggup dituliskan sebagai berikut.
L= {(x, y) | x2 + y2 = r2}
Pandang titik P1(x1, y1) pada ΔOP1P'1. Pada segitiga tersebut berlaku x12 + y12 = r12.
Pandang titik P2(x2, y2) pada ΔOP2P2'. Pada segitiga tersebut berlaku x22 + y22 = r22, dan seterusnya. Secara umum untuk setiap titik P(x, y) pada bundar ini berlaku x2 + y2 = r2.
Jadi, persamaan bundar yang berpusat di O(0, 0) dan berjari-jari r ialah :
x2 + y2 = r2.
Contoh Soal 1
Tentukan persamaan bundar yang berpusat di (0, 0) dengan panjang jari-jari  .
.
Pembahasan 1
Jari-jari r =  sehingga
sehingga %5E%7B2%7D) = 12.
= 12.
Jadi, persamaan bundar berpusat di (0, 0) dengan jari-jari  adalah x2 + y2 = 12.
adalah x2 + y2 = 12.
Contoh Soal 2
Tentukan persamaan bundar yang berpusat di titik (0, 0) dan melalui titik (–6, –8).
Penyelesaian 2
Persamaan bundar berpusat di (0, 0) dengan jari-jari r ialah :
x2 + y2 = r2 .... (1)
Oleh lantaran bundar melalui titik (–6, –8) maka dengan mensubstitusikan (–6, –8) pada persamaan (1), diperoleh :
x2 + y2 = r2
↔ (–6)2 + (–8)2 = r2
↔ r2 = 36 + 64 = 100
↔ .r =  =10
=10
Kemudian, r2 = 100 substitusikan pada persamaan (1), diperoleh x2 + y2 = 100.
Jadi, persamaan lingkarannya adalah x2 + y2 = 100.
1.2. Persamaan Lingkaran dengan Pusat T (a, b) dan Berjari-Jari r
Diketahui, sebuah bundar berpusat di titik T(a,b) dengan jari-jari r menyerupai diperlihatkan pada Gambar 4.
Titik P(x, y) ialah titik sebarang pada lingkaran, garis g ialah garis yang melalui titik sentra T(a, b) dan sejajar dengan sumbu-x. Proyeksi titik P terhadap garis g ialah titik Q sehingga segitiga TPQ siku-siku di Q.
 |
| Gambar 4. Lingkaran dengan Pusat T (a, b) dan Berjari-Jari r. |
Diketahui jarak TQ = (x – a) dan jarak PQ = (y – b). Pada segitiga TPQ berlaku teorema Pythagoras sebagai berikut.
TP2 = TQ2 + PQ2 ↔ r2 = (x – a)2 + (y – b)2
Lingkaran L sanggup dituliskan sebagai berikut:
L: {(x, y)(x – a)2 + (y – b)2 = r2}
Jadi, persamaan bundar yang berpusat di T(a, b) dan berjari-jari r ialah :
(x – a)2 + (y – b)2 = r2
Selanjutnya, persamaan tersebut dinamakan persamaan bundar standar (baku).
Contoh Soal 3
Tentukan persamaan bundar yang berpusat di (2,–1) dengan jari-jari  .
.
Jawaban 3
Persamaan bundar standar (x – a)2 + (y – b)2 = r2
Untuk sentra (2,–1) dengan jari-jari  , diperoleh :
, diperoleh :
(x – 2)2 + (y – (–1))2 = %5E%7B2%7D) ↔ (x – 2 )2 + (y + 1)2 = 18
↔ (x – 2 )2 + (y + 1)2 = 18
Jadi, persamaan lingkarannya adalah (x – 2 )2 + (y + 1)2 = 18.
Contoh Soal 4
Penyelesaian 4
Rumus jarak dari titik T (x1, y1) ke garis ax + by + c = 0 ialah :
Jarak dari sentra T (3,–4) ke garis 4x – 3y – 49 = 0 ialah jari-jari lingkaran, yaitu :
Jadi, persamaan lingkarannya ialah :
(x – 3)2 + (y + 4)2 = 25.
1.3. Bentuk Umum Persamaan Lingkaran
Anda telah mempelajari persamaan bundar yang berpusat di titik T (a, b) dengan jari-jari r, yaitu :
(x – a)2 + (y – b)2 = r2
Jika persamaan tersebut diuraikan maka diperoleh :
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2 + y2 – 2ax – 2by + (a2 + b2 – r2) = 0
x2 + y2 + Ax + By + C = 0 dengan A = –2a; B = –2b; dan C = (a2 + b2 – r2); A, B, dan C bilangan real. Jadi,
x2 + y2 + Ax + By + C = 0
ialah persamaan bundar yang berpusat di T(a, b) dengan jari-jari r, A = –2a, B = –2b, C = a2 + b2 – r2, A, B, dan C bilangan real.
Cobalah Anda ubah persamaan lingkaran x2 + y2 + Ax + By + C = 0 ke dalam bentuk kuadrat sempurna. Tuliskan langkah-langkahnya di buku kiprah Anda, kemudian kumpulkan pada guru Anda.
Jika bentuk umum persamaan bundar itu diubah dalam bentuk kuadrat tepat maka diperoleh :
x2 + y2 + Ax + By + C = 0
(x2 + Ax) + (y2 + By) = – C
Dari persamaan tersebut, diperoleh sentra lingkaran ) dan jari-jari lingkaran
dan jari-jari lingkaran 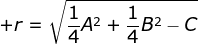
Contoh Soal 5
Tentukan sentra dan jari-jari lingkaran x2 + y2 – 4x + 6y – 3 = 0.
Jawaban 5
Bentuk umum persamaan bundar ialah :
x2 + y2 + Ax + By + C = 0
Dengan demikian, A = –4, B = 6, dan C = –3.
Contoh Soal 6
Tentukan sentra dan jari-jari bundar 2x2 + 2y2 – 4x –12y = 101.
Penyelesaian 6
Ubahlah persamaan pada soal menjadi bentuk umum, menyerupai berikut.
2x2 + 2y2 – 4x – 12y – 101 = 0 ↔ x2 + y2 – 2x – 6y – ( ) = 0
) = 0
Dengan demikian, A = –2, B = –6, dan C = – ( )
)
1.4. Posisi Titik terhadap Lingkaran
Bentuk geometris persamaan lingkaran (x– 2)2 + (y – 2)2 = 9 diperlihatkan pada Gambar 5.
Pada gambar itu tampak bahwa titik P1 (1, 3) terletak di dalam lingkaran, titik P2 (5, 2) terletak pada lingkaran, sedangkan titik P3 (6, –3) terletak di luar lingkaran.
 |
| Gambar 5. Bentuk geometris persamaan lingkaran (x– 2)2 + (y – 2)2 = 9. |
Anda sanggup mengetahui posisi titik P(x1, y1) terhadap bundar yang berpusat di T(a, b) berjari-jari r hanya dengan mengetahui jarak titik P(x1, y1) ke sentra bundar T(a, b).
 |
| Gambar 6. Posisi titik P(x1, y1) terhadap bundar yang berpusat di T(a, b) berjari-jari r. |
• Jika jarak titik P(x1, y1) ke sentra bundar T(a, b) kurang dari jari-jari bundar maka titik P(x1, y1) berada di dalam bundar menyerupai diperlihatkan pada Gambar 6(a). Secara matematis ditulis |PT| < r
(x1 – a)2 + (y1 – b)2 < r2 atau,
x12 + y12 + Ax1 + By1 + C < 0 • Jika jarak titik P(x1, y1) ke sentra bundar T(a, b) sama dengan jari-jari bundar maka titik P(x1, y1) berada pada bundar menyerupai diperlihatkan pada Gambar 6(b).
Secara matematis, ditulis |PT| = r
(x1 – a)2 + (y1 – b)2 = r2 atau,
x12 + y12 + Ax1 + By1 + C = 0 • Jika jarak titik P(x1, y1) ke sentra bundar T(a, b) lebih dari jari-jari bundar maka titik P(x1, y1) berada di luar bundar menyerupai diperlihatkan pada Gambar 6(c).
Secara matematis ditulis |PT| > r
(x1 – a)2 + (y1 – b)2 > r2 atau,
x12 + y12 + Ax1 + By1 + C > 0Contoh Soal 7
Tentukanlah posisi titik A(5, 1), B(4, –4), dan C(6, 3) terhadap bundar dengan persamaan x2 + y2 – 4x + 6y – 12 = 0.
Jawaban 7
Persamaan lingkaran x2 + y2 – 4x + 6y – 12 = 0 sanggup diubah sebagai berikut.
x2 + y2 – 4x + 6y – 12 = 0
(x2 – 4x) + (y2 + 6y) – 12 = 0
(x2 – 4x + 4) + (y2 + 6y + 9) – 12 = 0 + 4 + 9 ... kedua ruas ditambah 4 dan 9
(x – 2)2 + (y + 3)2 – 12 = 13
(x – 2)2 + (y + 3)2 = 25 Titik A (5, 1) terletak pada bundar sebab (5 – 2)2 + (1 + 3)2 = 25.
Titik B (4, –4) terletak di dalam bundar alasannya :
(4 – 2)2 + (–4 + 3)2 < 25.
Titik C (6, 3) terletak di luar bundar alasannya :
(6 – 2)2 + (3 + 3)2 > 25.
1.5. Posisi Garis terhadap Lingkaran
Diketahui garis g: y = mx + n, dan bundar :
L: x2 + y2 + Ax + By + C = 0.
Perpotongan garis g dengan bundar L ialah :
x2 + y2 + Ax + By + C = 0
x2 + (mx + n)2 + Ax + B (mx + n) + C = 0
x2 + m2x2 + 2mnx + n2 + Ax + Bmx + Bn + C = 0
(1 + m2)x2 + (2mn + A + Bm)x + n2 + Bn + C = 0 Nilai diskriminan persamaan kuadrat tersebut ialah :
D = b2 – 4ac
D = (2mn + A + Bm)2 – 4(1 + m2) (n2 + Bn + C) • Jika D > 0, diperoleh dua buah akar real yang berlainan.
Secara geometris, garis g: y = mx + n akan memotong lingkaran x2 + y2 + Ax + By + C = 0 di dua titik yang berlainan, menyerupai pada Gambar 7(a).
• Jika D = 0, diperoleh dua buah akar real yang sama.
Secara geometris, garis g: y = mx + n akan memotong lingkaran x2 + y2 + Ax + By + C = 0, di satu titik. Dikatakan garis g menyinggung bundar tersebut, menyerupai diperlihatkan pada Gambar 7(b).
• Jika D < 0, diperoleh dua buah akar imajiner yang berlainan. Secara geometris, garis g : y = mx + n tidak memotong atau menyinggung lingkaran x2 + y2 + Ax + By + C = 0 menyerupai diperlihatkan pada Gambar 7(c).
 |
| Gambar 7. Posisi Garis terhadap Lingkaran. |
Contoh Soal 8
Diketahui garis lurus g dengan persamaan y = mx + 2 dan bundar L dengan persamaan x2 + y2 = 4. Agar garis g memotong bundar L di dua titik yang berbeda, tentukan nilai m yang memenuhi.
Jawaban 8
y = mx + 2 ; maka, y2 = (mx + 2)2 = m2 x2 + 4m x + 4
x2 + y2 = 4 ↔ x2 + m2x2 + 4mx + 4 = 4
↔ (1 + m2)x2 + 4mx = 0 Diskriminan D = (4m)2 – 4 (1 + m2) (0)
D = 16 m2
Agar garis g memotong bundar L di dua titik maka haruslah D > 0.
Dengan demikian, 16m2 > 0
↔ m2 > 0
↔ m > 0 Anda kini sudah mengetahui Persamaan Lingkaran. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.
Referensi Lainnya :
[1] http://en.wikipedia.org/wiki/File:The_Parthenon_in_Athens.jpg
Referensi Lainnya :
[1] http://en.wikipedia.org/wiki/File:The_Parthenon_in_Athens.jpg






No comments:
Post a Comment