Contoh Soal Limit Fungsi Trigonometri Aljabar, Pembahasan, Pengertian, Materi, Rumus, Teorema, Matematika, Cara Substitusi Langsung dan Memfaktorkan Sekawan, Tak Hingga - Anda telah mempelajari ari nilai fungsi f di a pada bahan Suku Banyak. Sebagai contoh, diketahui f(x) =  . Untuk x = –1 diperoleh f(–1) = 1. Untuk x = 1 diperoleh f(1) = 3. Berapakah nilai f untuk x = 0? Ternyata, Anda tidak sanggup memilih nilai f di x = 0 lantaran pembagian bilangan hanya terdefinisi bila pembagi tidak sama dengan 0. Akan tetapi, Anda masih sanggup mempelajari bagaimana nilai f bila x mendekati 0 dengan memakai limit. Konsep limit suatu fungsi sanggup dipakai untuk menuntaskan permasalahan berikut. Misalkan persamaan posisi motor sesudah bergerak t jam dinyatakan oleh S = f(t) = 24t2 + 4t. Kecepatan motor pada ketika t = 1 jam sanggup diperoleh dari limit kecepatan rata-rata dalam selang t = 1 hingga t = 1 + Dt dengan mengambil Dt mendekati nol (Dt → 0). Pernyataan tersebut sanggup dinyatakan secara matematis sebagai berikut.
. Untuk x = –1 diperoleh f(–1) = 1. Untuk x = 1 diperoleh f(1) = 3. Berapakah nilai f untuk x = 0? Ternyata, Anda tidak sanggup memilih nilai f di x = 0 lantaran pembagian bilangan hanya terdefinisi bila pembagi tidak sama dengan 0. Akan tetapi, Anda masih sanggup mempelajari bagaimana nilai f bila x mendekati 0 dengan memakai limit. Konsep limit suatu fungsi sanggup dipakai untuk menuntaskan permasalahan berikut. Misalkan persamaan posisi motor sesudah bergerak t jam dinyatakan oleh S = f(t) = 24t2 + 4t. Kecepatan motor pada ketika t = 1 jam sanggup diperoleh dari limit kecepatan rata-rata dalam selang t = 1 hingga t = 1 + Dt dengan mengambil Dt mendekati nol (Dt → 0). Pernyataan tersebut sanggup dinyatakan secara matematis sebagai berikut.
-f%5Cleft+(+1+%5Cright+)%7D%7B%5CDelta+t%7D)
Dengan memakai konsep limit, Anda sanggup memilih kecepatan pada ketika t = 1 jam.
Untuk mempermudah Anda dalam mempelajari penggalan ini, pelajarilah diagram alur yang disajikan sebagai berikut.
A. Limit Fungsi
Dalam kehidupan sehari-hari, seringkali Anda mendengar kata-kata hampir atau mendekati. Misalnya, Ronaldo hampir mencetak gol, kecepatan motor itu mendekati 120 km/jam, dan sebagainya. Kata hampir atau mendekati dalam matematika disebut limit.
1. Pengertian Limit
Dalam matematika, limit merupakan nilai hampiran suatu variabel pada suatu bilangan real.
Notasi dijabarkan sebagai "limit fungsi f(x) pada ketika x mendekati a sama dengan L". Suatu limit dikatakan ada bila limit tersebut mempunyai limit kiri dan limit kanan yang sama. Limit kiri yaitu pendekatan nilai fungsi real dari sebelah kiri yang dinotasikan ) . Sedangkan limit kanan yaitu pendekatan nilai fungsi real dari sebelah kanan yang dinotasikan
. Sedangkan limit kanan yaitu pendekatan nilai fungsi real dari sebelah kanan yang dinotasikan ) . Untuk lebih memahaminya perhatikan uraian berikut. Misal, diberikan suatu limit fungsi
. Untuk lebih memahaminya perhatikan uraian berikut. Misal, diberikan suatu limit fungsi
Untuk mengetahui apakah limit tersebut ada, selidiki apakah limit kanan dan limit kirinya sama.
•  4x = 4 (4) = 16, lantaran x < 4
4x = 4 (4) = 16, lantaran x < 4
•  4x + 6 =
4x + 6 =  4x +
4x +  6= 16 + 6 = 22
6= 16 + 6 = 22
Oleh lantaran nilai limit kiri dan nilai limit kanan berbeda, limit fungsi tersebut tidak ada.
Selanjutnya, perhatikan bentuk fungsi berikut.
Limit fungsi tersebut, tidak terdefinisi di x = 3 lantaran kawasan asal fungsi f adalah{x | x ≠ 3).
Untuk mengetahui apakah limit tersebut ada, selidiki apakah limit kanan dan limit kirinya sama, menyerupai pada tabel berikut.
Tabel 1.
x | 2,99 | 2,999 | 2,9999 → | ← 3,0001 | 3,001 | 3,01 | |
5,99 | 5,999 | 5,9999 → | ← 6,0001 | 6,001 | 6,01 |
Berdasarkan tabel di atas, sanggup Anda ketahui bahwa pada ketika x mendekati 3, nilai fungsi f(x) mendekati 6.
Jadi,
Oleh lantaran x + 3 mendekati 6 bila x mendekati 3 maka  mendekati 6 bila x mendekati 3.
mendekati 6 bila x mendekati 3.
Meskipun fungsi f(x) tidak terdefinisi untuk x = 3, tetapi fungsi tersebut mendekati nilai 6 pada ketika x mendekati 3. Dengan demikian, sanggup dikatakan bahwa nilai limit fungsi tersebut yaitu 6.
Selanjutnya, perhatikan pula bentuk fungsi berikut.
Untuk mengetahui apakah limit tersebut ada, selidiki apakah limit kanan dan limit kirinya sama, menyerupai pada tabel berikut.
Tabel 2.
x | 2,99 | 2,999 | 2,9999 → | ← 3,0001 | 3,001 | 3,01 | |
5,99 | 5,999 | 5,9999 → | ← 6,0001 | 6,001 | 6,01 |
Berdasarkan tabel di atas, sanggup Anda ketahui bahwa pada ketika x mendekati 3, nilai fungsi f(x) mendekati 6. Jadi,
Dapat disimpulkan bahwa limit 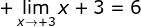 dapat diperoleh tanpa memakai Tabel 7.2. Ketika x mendekati 3, nilai x + 3 akan mendekati 6.
dapat diperoleh tanpa memakai Tabel 7.2. Ketika x mendekati 3, nilai x + 3 akan mendekati 6.
Dengan demikian sanggup disimpulkan bahwa :
Secara umum,  f(x) = L mengandung arti bahwa bila x mendekati atau menuju ke a, tetapi berlainan dengan a maka f(x) menuju ke L.
f(x) = L mengandung arti bahwa bila x mendekati atau menuju ke a, tetapi berlainan dengan a maka f(x) menuju ke L.
Contoh Soal Limit Fungsi 1 :
Tentukan limit berikut.
1.  (2x – 4)
(2x – 4)
2.  (x2 – 5x + 6)
(x2 – 5x + 6)
Pembahasan Soal Limit Fungsi :
1.  (2x – 4), artinya bila x mendekati 2 maka (2x – 4) mendekati (2 · 2 – 4) = 0. Dengan demikian,
(2x – 4), artinya bila x mendekati 2 maka (2x – 4) mendekati (2 · 2 – 4) = 0. Dengan demikian,  (2x – 4) = 0.
(2x – 4) = 0.
2.  (x2 – 5x + 6), artinya bila x mendekati 4 maka (x2 – 5x + 6) akan mendekati (42 – 5.4 + 6) = 2. Jadi,
(x2 – 5x + 6), artinya bila x mendekati 4 maka (x2 – 5x + 6) akan mendekati (42 – 5.4 + 6) = 2. Jadi,  x2 – 5x + 6) = 2.
x2 – 5x + 6) = 2.
Contoh Soal 2 :
Diketahui f (x) = 
Tentukan:
a. nilai fungsi di titik 0
b. nilai limit di titik 0.
Penyelesaian :
a. f(0) = 5
b. 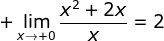
Contoh Soal 3 :
Diketahui limit 
Tentukan nilai limit tersebut.
Jawaban :
= 5 + 5
= 10
Ingatlah :
Untuk menghitung  , sebaiknya
, sebaiknya  difaktorkan, kemudian disederhanakan, sebelum menyubstitusikan x = 0 lantaran bila x = 0 disubstitusikan secara pribadi maka diperoleh
difaktorkan, kemudian disederhanakan, sebelum menyubstitusikan x = 0 lantaran bila x = 0 disubstitusikan secara pribadi maka diperoleh 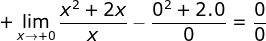 dan ini bentuk tidak tentu.
dan ini bentuk tidak tentu.
2. Limit Fungsi Aljabar
Limit konstanta k unk tuk x mendekati a ada dan nilainya sama dengan k, ditulis  k = k. Secara grafik, hal tersebut sanggup Anda lihat pada Gambar 1.
k = k. Secara grafik, hal tersebut sanggup Anda lihat pada Gambar 1.
Pandang fungsi f(x) = k maka  f(x) =
f(x) =  k = k. Limit x untuk x mendekati a pun ada dan nilainya sama dengan a, ditulis
k = k. Limit x untuk x mendekati a pun ada dan nilainya sama dengan a, ditulis  x = a.
x = a.
 |
| Gambar 1. Grafik fungsi f(x) = k. |
Untuk mengetahui adanya limit secara mudah, Anda sanggup memakai teorema berikut.
Teorema Limit Utama
Jika f (x) dan g(x) yaitu fungsi dan k konstanta maka :
1.  (f (x) + g(x)) =
(f (x) + g(x)) =  f (x) +
f (x) +  g(x)
g(x)
2.  (f (x) – g(x)) =
(f (x) – g(x)) =  f (x) –
f (x) –  g(x)
g(x)
3.  (f (x) · g(x)) =
(f (x) · g(x)) =  f (x) .
f (x) .  g(x)
g(x)
4. %7D%7Bg%5Cleft+(+x+%5Cright+)%7D%3D%5Cfrac%7B%5Clim_%7Bx%5Crightarrow+a%7Df%5Cleft+(+x+%5Cright+)%7D%7B%5Clim_%7Bx%5Crightarrow+a%7Dg%5Cleft+(+x+%5Cright+)%7D) ; g(x) ≠ 0
; g(x) ≠ 0
5.  k f (x) = k
k f (x) = k  f (x); k = konstanta
f (x); k = konstanta
6.  [f (x)]n =
[f (x)]n = ; dengan n bilangan lingkaran positif
; dengan n bilangan lingkaran positif
7. %7D=%5Csqrt%5Bn%5D%7B%5Clim_%7Bx%5Crightarrow+a%7Df%5Cleft+(+x+%5Cright+)%7D) ; dengan
; dengan  f (x) ≥ 0
f (x) ≥ 0
a. Cara Menentukan Limit dengan Substitusi Langsung
Ada beberapa fungsi yang nilai limitnya sanggup ditentukan dengan cara substitusi pribadi menyerupai pola berikut.
Contoh Soal Limit Fungsi Aljabar 4 :
Tentukan limit fungsi-fungsi berikut.
1.  (x3 + 4x + x - 6)
(x3 + 4x + x - 6)
2. 
Penyelesaian Soal Limit Fungsi Aljabar :
1.  (x3 + 4x + x - 6) = (–4)3 + 4(–4)2 + (–4) – 6 = –10
(x3 + 4x + x - 6) = (–4)3 + 4(–4)2 + (–4) – 6 = –10
2. 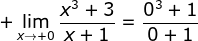 = 1
= 1
b. Menentukan Limit dengan Cara Memfaktorkan Terlebih Dahulu
Jika dengan cara substitusi pribadi pada %7D%7Bg%5Cleft+(+x+%5Cright+)%7D) diperoleh bentuk
diperoleh bentuk  (bentuk tak tentu), lakukan pemfaktoran terlebih dahulu terhadap f (x) dan g(x). Kemudian, sederhanakan ke bentuk paling sederhana. Agar lebih jelas, perhatikan uraian berikut.
(bentuk tak tentu), lakukan pemfaktoran terlebih dahulu terhadap f (x) dan g(x). Kemudian, sederhanakan ke bentuk paling sederhana. Agar lebih jelas, perhatikan uraian berikut.
%7D%7Bg%5Cleft+(+x+%5Cright+)%7D=%5Clim_%7Bx%5Crightarrow+a%7D%5Cfrac%7B%5Cleft+(+x-a+%5Cright+)P%5Cleft+(+x+%5Cright+)%7D%7B%5Cleft+(+x-a+%5Cright+)Q%5Cleft+(+x+%5Cright+)%7D%3D%5Clim_%7Bx%5Crightarrow+a%7D%5Cfrac%7BP%5Cleft+(+x+%5Cright+)%7D%7BQ%5Cleft+(+x+%5Cright+)%7D%3D%5Cfrac%7BP%5Cleft+(+a+%5Cright+)%7D%7BQ%5Cleft+(+a+%5Cright+)%7D)
Dalam hal ini P(a) ≠ 0 dan Q(a) ≠ 0.
Pertanyaan: Mengapa f (x) dan g(x) boleh dibagi oleh (x – a)?
Aktivitas Matematika
Bersama kelompok mencar ilmu Anda, lakukan acara menghitung limit bentuk  . Permasalahannya yaitu menentukan
. Permasalahannya yaitu menentukan  . Langkah-langkah yang sanggup Anda lakukan yaitu sebagai berikut.
. Langkah-langkah yang sanggup Anda lakukan yaitu sebagai berikut.
Langkah ke-1
Menyubstitusikan x = 1 ke dalam fungsi yang dicari nilai limitnya, yaitu :
Langkah ke-2
Agar tidak muncul bentuk  faktorkanlah x2 – 1, kemudian sederhanakan sebagai berikut.
faktorkanlah x2 – 1, kemudian sederhanakan sebagai berikut.
Langkah ke-3
Setelah fungsi yang dicari limitnya disederhanakan, substitusikan x = 1 pada limit fungsi yang sederhana itu, sebagai berikut.
Jadi, 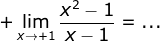
Contoh soal 6 :
Tentukan limit fungsi-fungsi berikut.
1. 
2. 
3. 
Pembahasan :
1. Jika dengan cara substitusi langsung, diperoleh :
2. Dengan cara substitusi langsung, diperoleh :
Agar tidak muncul bentuk  , faktorkanlah x + 3 sebagai berikut.
, faktorkanlah x + 3 sebagai berikut.
3. Coba Anda kerjakan dengan cara substitusi langsung. Apakah diperoleh bentuk  . Agar tidak muncul bentuk
. Agar tidak muncul bentuk , faktorkanlah (3x3 + 3x) dan (2x3 – 8x) sebagai berikut.
, faktorkanlah (3x3 + 3x) dan (2x3 – 8x) sebagai berikut.
c. Menentukan Limit dengan Mengalikan Faktor Sekawan
Jika pada %7D%7Bg%5Cleft+(+x+%5Cright+)%7D) diperoleh bentuk tak tentu
diperoleh bentuk tak tentu  . untuk x = a dan sulit untuk memfaktorkan f(x) dan g(x), lakukan perkalian dengan faktor sekawan dari g(x) atau f(x). Agar lebih jelas, pelajari pola berikut.
. untuk x = a dan sulit untuk memfaktorkan f(x) dan g(x), lakukan perkalian dengan faktor sekawan dari g(x) atau f(x). Agar lebih jelas, pelajari pola berikut.
Contoh Soal 7 :
Tentukan limit berikut.
a.
b.
Jawaban :
1. Jika dengan cara substitusi langsung, diperoleh :
Agar tidak muncul bentuk tak tentu, kalikanlah  dengan
dengan  , sebagai berikut.
, sebagai berikut.
2. Coba Anda kerjakan dengan cara substitusi langsung. Apakah diperoleh bentuk  ? Agar tidak muncul bentuk
? Agar tidak muncul bentuk  kalikanlah
kalikanlah  dengan faktor sekawannya, sebagai berikut.
dengan faktor sekawannya, sebagai berikut.
3. Limit Tak Hingga dan Limit Fungsi di Tak Hingga
Lambang ∞ (dibaca: tak hingga) dipakai untuk menyatakan nilai bilangan yang semakin besar. Jadi, ∞ bukan merupakan lambang bilangan dan tidak sanggup dioperasikan secara aljabar sehingga tidak benar ∞ – ∞ = 0 atau  = 1.
= 1.
Amati fungsi berikut.
Fungsi f tidak terdefinisi di x = 0 lantaran pembagian bilangan satu hanya terdefinisi bila pembagi ≠ 0. Anda sanggup memilih f (x) = =%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D) pada beberapa nilai x yang mendekati 0 menyerupai diperlihatkan pada Tabel 3.
pada beberapa nilai x yang mendekati 0 menyerupai diperlihatkan pada Tabel 3.
x | |
–0,01 | 10.000 |
–0,001 | 1.000.000 |
–0,0001 | 100.000.000 |
–0,00001 | 10.000.000.000 |
0 | ? |
0,00001 | 10.000.000.000 |
0,0001 | 100.000.000 |
0,001 | 1.000.000 |
0,01 | 10.000 |
Amati tabel tersebut. Jika x menuju 0 maka nilai  bernilai positif yang semakin membesar tanpa batas. Dalam lambang matematika ditulis
bernilai positif yang semakin membesar tanpa batas. Dalam lambang matematika ditulis 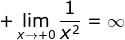 .
.
Bentuk grafik fungsi menyerupai ini diperlihatkan pada Gambar 2.
 |
| Gambar 2. Grafik f(x) = |
Tabel 4. memperlihatkan nilai  untuk nilai x yang menjadi sangat besar.
untuk nilai x yang menjadi sangat besar.
Tabel 4.
x | 1 | 10 | 1.000 | 10.000 | 100.000 | ? |
1 | 0,01 | 0,000001 | 0,00000001 | 0,0000000001 | 0 |
Amatilah tabel tersebut, ternyata nilai  menuju 0 bila x menjadi sangat besar. Dalam lambang matematika, ditulis
menuju 0 bila x menjadi sangat besar. Dalam lambang matematika, ditulis 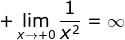 .
.
Lain halnya dengan fungsi f (x) = x2. Ketika x menjadi sangat besar maka nilai x2 pun bernilai semakin besar tanpa batas. Dalam lambang matematika, ditulis :
(Amati kembali Gambar 2)
Untuk fungsi g(x) =
Untuk menuntaskan limit fungsi tak hingga Anda sanggup memakai Teorema Limit Utama. Pelajari contoh-contoh berikut.
Perhatikan, ketika x semakin membesar tanpa batas, nilai  menuju 1, sedangkan nilai
menuju 1, sedangkan nilai  menuju nol. Akibatnya, nilai
menuju nol. Akibatnya, nilai  membesar tanpa batas.
membesar tanpa batas.
Dengan demikian, 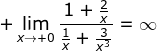
Dari uraian tersebut, dapatkah Anda menduga bentuk umum limit? Cobalah nyatakan bentuk tersebut dengan kata-kata Anda sendiri. Konsep limit yang telah Anda pelajari tersebut memperjelas ketentuan limit berikut.
Ingatlah :
Dari Gambar 2, bila x menjadi sangat kecil (x → ∞) maka nilai  menuju 0. Dalam lambang matematika ditulis
menuju 0. Dalam lambang matematika ditulis  = 0.
= 0.
Contoh Soal 8 : Soal SKALU, 1978
Penyelesaian :
Ingatlah :
Pada soal a, pembilang dan penyebut bentuk  masing-masing dibagi dengan x lantaran bila disubstitusikan secara pribadi diperoleh bentuk
masing-masing dibagi dengan x lantaran bila disubstitusikan secara pribadi diperoleh bentuk  . Dengan kebijaksanaan budi yang sama, pembilang dan penyebut fungsi pada soal b, c, d, dan e masing-ma sing harus dibagi dengan pangkat tertinggi dari pembilang
. Dengan kebijaksanaan budi yang sama, pembilang dan penyebut fungsi pada soal b, c, d, dan e masing-ma sing harus dibagi dengan pangkat tertinggi dari pembilang
biar tidak diperoleh bentuk  .
.
Secara umum,
• %7D%7Bg%5Cleft+(+x+%5Cright+)%7D=%5Cfrac%7Bkoefisien%5C:+pangkat%5C:+tertinggi%5C:+f%5Cleft+(+x+%5Cright+)%7D%7Bkoefisien%5C:+pangkat%5C:+tertinggi%5C:+g%5Cleft+(+x+%5Cright+)%7D) , bila pangkat tertinggi f(x) = pangkat tertinggi g(x);
, bila pangkat tertinggi f(x) = pangkat tertinggi g(x);
• %7D%7Bg%5Cleft+(+x+%5Cright+)%7D=0) = 0, bila pangkat tertinggi f(x) < pangkat tertinggi g(x);
= 0, bila pangkat tertinggi f(x) < pangkat tertinggi g(x);
• %7D%7Bg%5Cleft+(+x+%5Cright+)%7D=%5Cpm+%5Cinfty) , bila pangkat tertinggi f(x) > pangkat tertinggi g(x);
, bila pangkat tertinggi f(x) > pangkat tertinggi g(x);
dengan f(x) dan g(x) keduanya merupakan fungsi polinom.
Cara lain untuk memperoleh penyelesaian limit fungsi yaitu mengalikan dengan faktor sekawan. Pelajari contoh-contoh berikut.
Informasi untuk Anda :
Lambang tak hingga yang dipakai kini (∞), kali pertama diperkenalkan oleh John Wallis (1616–1703) pada tahun 1655 dalam jurnalnya yang berjudul On Conic Sections. (Sumber: www.DrMath.com)
Pada Subbab A telah dipelajari limit fungsi aljabar. Kali ini akan dipelajari limit fungsi trigonometri. Awali penggalan ini dengan mempelajari sifat berikut.
1. Menentukan Rumus Limit Fungsi Trigonometri Sifat Prinsip Apit
Amati Gambar 3.
Diketahui f, g, dan h yaitu fungsi-fungsi yang memenuhi f (x) ≤ g(x) ≤ h(x) untuk semua x bersahabat a, kecuali mungkin di a. Jika  f (x) =
f (x) =  h(x) = L maka g(x) = L.
h(x) = L maka g(x) = L.
 |
| Gambar 3. Grafik f, g, dan h yaitu fungsifungsi yang memenuhi f (x) ≤ g(x) ≤ h(x) untuk semua x bersahabat a, kecuali mungkin di a. |
Sekarang amati Gambar 4(a). Diketahui, 0 < t<  . Ketika t → 0 maka titik P bergerak ke arah A(1, 0) sehingga :
. Ketika t → 0 maka titik P bergerak ke arah A(1, 0) sehingga :
Perpanjangan  dan garis tegak lurus sumbu-x yang melalui A akan berpotongan di titik T(1, tan t) menyerupai diperlihatkan pada Gambar 4 (b).
dan garis tegak lurus sumbu-x yang melalui A akan berpotongan di titik T(1, tan t) menyerupai diperlihatkan pada Gambar 4 (b).
 |
| Gambar 4. Grafik Limit Fungsi Trigonometri. |
Sekarang amati ∆OAP, tembereng OAP, dan ∆OAT pada Gambar 4(b). Dari hasil pengamatan tentunya Anda memahami bahwa :
luas ∆OAP ≤ luas juring OAP ≤ luas ∆OAT ....(1)
Anda ketahui:
luas ∆OAP = 1/2 alas × tinggi = 1/2 x 1 x sin t = 1/2 sin t,
luas juring OAP = 1/2 x jari-jari × sudut dalam radian = 1/2 x 12 x t = 1/2t, dan
luas ∆OAT = 1/2 ganjal × tinggi = 1/2 x 1 x tan t = 
Dengan demikian, ketidaksamaan (1) sanggup dituliskan sebagai :
Kalikan ketidaksamaan (2) dengan bilangan positif  , diperoleh :
, diperoleh :
Sampai uraian ini anggaplah 0 < t <  . Akan tetapi, jika
. Akan tetapi, jika  < t < 0 maka 0 < –t <
< t < 0 maka 0 < –t <  sehingga cos (–t) ≤
sehingga cos (–t) ≤ %7D%7B-t%7D) ≤ 1
≤ 1
cos t ≤  ≤ 1 ....(3)
≤ 1 ....(3)
Dalam ketidaksamaan (3), misalkan t → 0, f (t) = cos t, g(t) =  , dan h(t) = 1.
, dan h(t) = 1.
Anda tentu memahami bahwa  f(t) ≤
f(t) ≤  g(t) ≤
g(t) ≤  h(t).
h(t).
Untuk t = 0 maka f(t) cos t = cos 0 = 1 dan lantaran h(t) = 1 maka 1 ≤  ≤ 1. Dalam hal ini tidak ada kemungkinan lain kecuali
≤ 1. Dalam hal ini tidak ada kemungkinan lain kecuali  = 1. Dengan demikian,
= 1. Dengan demikian,  g(t) =
g(t) =  = 1.
= 1.
Dapatkah Anda mengambarkan bahwa :

Silakan buktikan sendiri.
2. Cara Menentukan Limit Fungsi Trigonometri
Setelah Anda memahami rumus limit fungsi trigonometri, pelajari cara memilih limit fungsi trigonometri tersebut. Dalam beberapa hal, cara menghitung limit fungsi trigonometri sama dengan cara menghitung limit fungsi aljabar. Oleh lantaran itu, teorema limit utama pada Subbab A.2 berlaku juga untuk limit fungsi trigonometri.
Contoh Soal Limit Fungsi Trigonometri 9 :
Hitunglah limit fungsi trigonometri berikut.
1. 
2. 
Penyelesaian :
1.  = 1 (sesuai rumus)
= 1 (sesuai rumus)
Contoh Soal 10 :
Hitunglah limit fungsi trigonometri berikut.
a. 
b. 
c. 
Contoh Soal 11 :
Tentukanlah -f%5Cleft+(+x+%5Cright+)%7D%7Bh%7D) bagi fungsi-fungsi berikut ini.
bagi fungsi-fungsi berikut ini.
1. f(x) = cos x
2. f(x) = sin x
Jawaban :
Contoh Soal 12 :
Hitunglah limit fungsi trigonometri berikut.
a. 
b. 
Contoh Soal 13 :
Hitunglah:
a.  tan 3x sec 2x
tan 3x sec 2x
b.  (cosec2 x - cos ec x cos x)
(cosec2 x - cos ec x cos x)
Contoh Soal 14 : Soal UMPTN 1998
Anda kini sudah mengetahui Limit Fungsi. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.















No comments:
Post a Comment