Rumus Turunan Fungsi, Contoh Soal, Konsep, Cara Menentukan, Persamaan Garis Singgung, Kecepatan Sesaat, Bilangan Rasional, Pembahasan, Notasi Leibnitz, Matematika - Pembahasan limit fungsi yang telah Anda pelajari di materi sebelumnya sanggup dikembangkan pada pembahasan turunan fungsi sebab dengan mengetahui turunan fungsi, Anda sanggup mempelajari sifat-sifat fungsi. Sifat-sifat fungsi tersebut misalnya, kemonotonan fungsi, ekstrim fungsi, kecukupan fungsi, dan titik balik fungsi. Di samping itu, Anda juga sanggup mengaitkan turunan fungsi dengan kecepatan sesaat serta sanggup memakai turunan fungsi untuk mempelajari aplikasi permasalahan sederhana, ibarat permasalahan berikut. Banyak minyak pelumas (selama satu tahun) yang dipakai oleh suatu kendaraan yang bergerak dengan kecepatan v km/jam memenuhi persamaan Q(v) =  x2 + 2x - 20 liter. Dengan memahami konsep turunan, Anda sanggup memilih jumlah maksimum minyak pelumas yang dipakai dalam 4 tahun.
x2 + 2x - 20 liter. Dengan memahami konsep turunan, Anda sanggup memilih jumlah maksimum minyak pelumas yang dipakai dalam 4 tahun.
Untuk mempermudah Anda dalam mempelajari potongan ini, pelajarilah diagram alur yang disajikan sebagai berikut.
A. Konsep Turunan
Untuk memahami konsep dasar turunan, tinjaulah dua problem yang kelihatannya berbeda. Masalah pertama ialah problem garis singgung, sedangkan problem kedua ialah problem kecepatan sesaat. Satu dari kedua problem itu menyangkut geometri dan lainnya yang menyangkut mekanika terlihat ibarat tidak ada hubungan. Sebenarnya, kedua problem itu merupakan kembaran yang identik. Agar lebih jelasnya, pelajari uraian berikut.
1. Garis Singgung
Misalkan A ialah suatu titik tetap pada grafik y = f(x) dan B ialah sebuah titik berdekatan yang sanggup dipindah-pindahkan sepanjang grafik y = f(x). Misalkan, titik A berkoordinat (a, f(a)) maka titik B berkoordinat (a + Δx, f(a + Δx)). Garis yang melalui A dan B mempunyai gradien (kemiringan) -f%5Cleft+(+a+%5Cright+)%7D%7B%5CDelta+x%7D) . Garis ini memotong grafik di dua titik A dan B yang berbeda.
. Garis ini memotong grafik di dua titik A dan B yang berbeda.
Jika titik B bergerak sepanjang kurva y = f(x) mendekati titik A maka nilai Δx semakin kecil. Jika nilai Δx mendekati nol maka titik B akan berimpit dengan titik A. Akibatnya, garis singgung (jika tidak tegak lurus pada sumbu-x) ialah garis yang melalui A(a, f(a)) dengan gradien :
Pertanyaan: Mengapa persamaan garis singgung dihentikan tegak lurus sumbu-x?
 |
| Gambar 2. Garis singgung dihentikan tegak lurus sumbu-x. |
Contoh Soal 1 :
Tentukan gradien garis singgung pada kurva
a. f(x) = x2 di titik dengan absis 2
b. f(x) = x3 di titik dengan absis 3
Penyelesaian :
a.
Jadi, gradien garis singgung kurva f(x) = x2 di titik dengan absis x = 2 ialah m = 4.
b.
Jadi, gradien garis singgung kurva f(x) = x3 di titik dengan absis x = 3 ialah m = 27.
2. Kecepatan Sesaat
Misalkan, fungsi f(x) = 15x2 + 20x menyatakan jarak (dalam km) yang ditempuh sebuah kendaraan beroda empat sehabis x jam perjalanan selama selang waktu 0 ≤ x ≤ 2. Kecepatan rata-rata kendaraan beroda empat itu selama perjalanannya ialah :
= 50 km/jam
Sekarang, coba amati kecepatan rata-rata kendaraan beroda empat dalam selang c ≤ x ≤ d. Untuk keperluan ini, buatlah Tabel 1.
Tabel 1. Kecepatan rata-rata kendaraan beroda empat dalam selang c ≤ x ≤ d
Selang Waktu | |
0 – 1 | 35 |
0,8 – 1 | 47 |
0,9 – 1 | 48,5 |
0,99 – 1 | 49,85 |
0,999 – 1 | 49,9850 |
0,9999 – 1 | 49,9985 |
1 – 1,0001 | 50,0015 |
1 – 1,001 | 50,015 |
1 – 1,01 | 50,15 |
1 – 1,5 | 57,5 |
1 – 2 | 65 |
Amati tabel tersebut. Nilai  mendekat ke bilangan 50 bila lebar selang waktunya dibentuk semakin mengecil (Δx mendekati nol). Nilai 50 tersebut disebut kecepatan (sesaat) pada x = 1.
mendekat ke bilangan 50 bila lebar selang waktunya dibentuk semakin mengecil (Δx mendekati nol). Nilai 50 tersebut disebut kecepatan (sesaat) pada x = 1.
Sekarang, sanggup dipahami bahwa kecepatan sesaat diperoleh melalui proses limit terhadap kecepatan rata-rata dengan cara menciptakan nilai-nilai x mendekat ke-1 atau Δx erat ke nol. Dalam lambang matematika kecepatan sesaat pada x = 1 ditulis :
Jadi, kecepatan kendaraan beroda empat pada ketika x = 1 ialah 50 km/jam.
Dari uraian tersebut, dapatkah Anda menyatakan kecepatan sesaat v di x = a? Cobalah nyatakan dengan katakata Anda sendiri. Uraian tersebut menggambarkan definisi kecepatan sesaat v di x = a, yaitu
Sekarang, tentunya Anda sanggup melihat mengapa Anda menyebut kemiringan dari garis singgung dan kecepatan sesaat ialah kembaran identik. Amatilah kedua rumus tersebut, yaitu rumus (1) dan (2). Kedua rumus tersebut memakai nama berlainan untuk konsep yang sama, tetapi dalam situasi yang berlainan.
 |
| Gambar 3. Jarak yang ditempuh kendaraan beroda empat ini mengikuti fungsi f(x) = 15x2 + 20x. Berapakah kecepatan rata-ratanya? |
Contoh Soal 2 :
Sebuah benda bergerak sepanjang garis lurus sehingga kedudukannya sehabis x detik memenuhi persamaan f (x) = 6x3 + x2 , dengan f(x) dinyatakan dalam meter.
a. Tentukan kecepatan rata-rata benda dalam selang waktu 2 ≤ x ≤ 3.
b. Berapa kecepatan sesaat benda pada x = 2 detik?
Pembahasan :
a.
Jadi, kecepatan rata-ratanya ialah 119 m/s.
b.
Jadi, kecepatan pada ketika x = 2 atau pada detik kedua ialah 76 meter/detik.
3. Turunan Fungsi di x = a
Jika fungsi y = f(x) terdefinisi di sekitar x = a maka :
Jika  ada maka nilainya disebut turunan fungsi f(x) di x = a. Turunan fungsi f ialah suatu fungsi juga, yaitu fungsi turunan yang dilambangkan dengan f ‘(x). Untuk menyatakan turunan di x = a dinyatakan dengan f ‘(a). Jadi,
ada maka nilainya disebut turunan fungsi f(x) di x = a. Turunan fungsi f ialah suatu fungsi juga, yaitu fungsi turunan yang dilambangkan dengan f ‘(x). Untuk menyatakan turunan di x = a dinyatakan dengan f ‘(a). Jadi,
Contoh Soal 3 :
Gunakan konsep limit untuk menuntaskan soal berikut ini. Jika f (x) = x2 – x , tentukan f'(5).
Jawaban :
Contoh Soal 4 :
Tentukanlah f ‘(x) fungsi-fungsi berikut ini.
a. f(x) = x2 + x
b. f(x) = cos x
Penyelesaian :
a. f(x) = x2 + x
b. f(x) = cos x
Contoh Soal 5 : Panjang sebuah persegipanjang sama dengan tiga kali lebarnya. Tentukan laju perubahan luas terhadap lebar untuk lebar = 5 cm.
Jawaban :
Misalkan, lebar = l cm maka panjang = p = 3 × l = 3l dan luas =
L = p × l = 3l . l = 3l2.
Jadi, L = f (l) = 3l2.
Laju perubahan luas terhadap lebar l untuk l = 5 ialah L ‘(5).
4. Mengenal Notasi Leibnitz
Anda telah mempelajari bahwa turunan fungsi f(x) dinotasikan dengan f '(x). Nilai Δx menyatakan perubahan nilai x, yaitu Δx = x2 – x1. Adapun perubahan f(x + Δx) – f(x) menyatakan perubahan nilai fungsi f(x) dinotasikan dengan Δf. Selanjutnya, bentuk limit tersebut sanggup dituliskan menjadi :
Selain itu, terdapat notasi lain untuk menyatakan turunan fungsi, yaitu df/dx . Diketahui fungsi :
y = f(x) ....(1)
sehingga turunan fungsi (1) sanggup dituliskan menjadi :
Notasi tersebut diperkenalkan oleh spesialis matematika Jerman, yaitu Gottfried Wilhelm Leibnitz (1646–1716) sehingga dinamakan notasi Leibnitz, tepatnya notasi Double d Leibnitz.
Contoh Soal 6 :
Misalkan f(x) = x3 , tentukanlah :
a. df / dx
b. nilai x sehingga df / dx = 12
Penyelesaian :
a.
b. df / dx = 3x2 maka 3x2 = 12 ↔ x = ± 2.
Jadi, nilai x yang memenuhi df / dx = 12 adalah x = ± 2.
Contoh Soal 7 :
Sebuah benda bergerak sehingga jarak yang ditempuh memenuhi persamaan s = f(t) = t2 – 3t. Tentukanlah laju perubahan sesaat jarak terhadap waktu t. Tentukanlah nilai t sedemikian sehingga laju perubahan jarak terhadap waktu ialah 15.
Penyelesaian :
Laju perubahan sesaat jarak terhadap waktu ialah :
Apabila laju perubahan jarak terhadap waktu sama dengan 16, diperoleh :
df / dx = 2t – 3 ↔ 15 = 2t – 3
↔ 2t = 18 ↔ t = 9
Jadi, laju perubahan sama dengan 15 terjadi pada ketika t = 9 sekon.
B. Cara Menentukan Turunan Fungsi
Proses mendapat turunan suatu fungsi secara eksklusif yang memakai definisi turunan, yaitu dengan menyusun hasil bagi selisih -f%5Cleft+(+x+%5Cright+)%7D%7B%5CDelta+x%7D) dan menghitung limitnya, memakan waktu dan membosankan. Tentunya, Anda perlu menyebarkan cara atau proses yang akan memungkinkan
dan menghitung limitnya, memakan waktu dan membosankan. Tentunya, Anda perlu menyebarkan cara atau proses yang akan memungkinkan
Anda untuk memperpendek proses yang berkepanjangan itu.
Untuk itu, pelajari uraian berikut ini.
1. Menentukan Turunan Fungsi f(x) = axn
Misalkan, fungsi f(x) = axn dengan n = 1, 2, dan 3. Untuk n = 1, diperoleh f(x) = ax dan turunan fungsi tersebut ialah :
Untuk n = 2, diperoleh f (x) = ax2 dan turunan fungsi tersebut ialah :
Dengan cara yang sama, coba Anda cari turunan fungsi :
f(x) = ax3 , f(x) = ax4 dan f(x) = ax5.
Anda sanggup menurunkan hal ibarat ini untuk fungsi-fungsi berikut.
f(x) = ax6, f ‘(x) = 6ax5
.
.
.
f(x) = ax15, f ‘(x) = 15ax14
.
.
.
f(x) = axn, f ‘(x) = naxn – 1
Dari uraian tersebut, dapatkah Anda menduga bentuk umum turunan fungsi? Cobalah nyatakan bentuk tersebut dengan kata-kata Anda sendiri. Konsep yang telah Anda pelajari tersebut memperjelas kesimpulan berikut.
Misalkan, f(x) = axn , dengan n bilangan orisinil maka f '(x) = naxn – 1. Untuk n = 0, f(x) = axn menjadi f(x) = ax0 = a.
Fungsi f(x) = a dinamakan fungsi konstan sehingga untuk berapa pun nilai x, nilai fungsinya tetap, yaitu a. Turunan fungsi konstan ialah :
sehingga rumus tersebut berlaku untuk n bilangan lingkaran sebagai berikut.
Misalkan, f(x) = axn dengan n bilangan lingkaran maka f '(x) = anxn – 1 untuk f(x) = a, f '(x) = 0 dengan a sebarang bilangan real.
Contoh Soal 8 :
Tentukanlah turunan fungsi-fungsi berikut ini.
a. f(x) = x4
b. f(x) = –8x3
Jawaban :
a. f(x) = x4 maka f '(x) = 4x4–1 = 4x3
b. f(x) = –8x3 maka f ' (x) = –8(3)x3–1= –24x2
Contoh Soal 9 :
Tentukan df/dx untuk fungsi-fungsi berikut.
a. f (x) = ½ x2
b. g (x) = 
Jawaban :
Contoh Soal 10 :
Diketahui tinggi tubuh seorang anak pada usia 11 tahun hingga 12 tahun ialah tetap, yaitu T(t) = 120 cm. Tentukanlah laju pertumbuhan (laju pertumbuhan sesaat) tinggi tubuh anak tersebut. Jelaskan.
Pembahasan :
Tinggi tubuh anak tersebut pada usia 11 tahun hingga 12 tahun tetap. Oleh sebab itu, T(t) = 120 ialah fungsi konstan sehingga T ‘(t) = 0. Dengan kata lain, laju pertumbuhan tinggi tubuh anak tersebut ialah nol atau tinggi tubuh anak tersebut pada usia 11 tahun hingga 12 tahun tidak mengalami perubahan.
2. Menentukan Turunan Fungsi si f(x) = axn dengan n Bilangan Rasional
Misalkan, f(x) =  , turunan fungsi f(x) ialah :
, turunan fungsi f(x) ialah :
Dengan cara yang sama ibarat di atas, coba Anda cari turunan fungsi f(x) =  dan f(x) =
dan f(x) =  5.
5.
Dari uraian tersebut dapatkah Anda menduga bentuk umum turunan fungsi f(x) = axn ? Cobalah nyatakan bentuk tersebut dengan kata-kata Anda sendiri. Konsep turunan fungsi f(x) = axn yang telah Anda pelajari tersebut memperjelas kesimpulan berikut.
Misalkan, f(x) = axn , dengan n bilangan rasional maka turunannya ialah f '(x) = naxn – 1.
Contoh Soal 11 :
Tentukan turunan fungsi-fungsi berikut.
a. f(x) = 
b. f(x) = 
c. f(x) = 
Jawaban :
3. Turunan Fungsi Berbentuk y = u ± v
Diketahui, fungsi y = f(x) dengan f(x) = u(x) + v(x), dalam hal ini u(x) dan v(x) fungsi yang sanggup diturunkan di x = a untuk a bilangan real. Dengan demikian,
Dari uraian tersebut, dapatkah Anda menduga bentuk umum turunan fungsi y = u ± v? Cobalah nyatakan bentuk tersebut dengan kata-kata Anda sendiri. Konsep turunan fungsi y = u ± v yang telah Anda pelajari tersebut memperjelas kesimpulan berikut.
Misalkan, a ialah bilangan real sebarang sehingga berlaku y ' = f '(a) = u'(a) + v'(a) ; untuk y = u + v maka y' = u' + v'
Dengan cara yang sama, coba Anda tunjukkan bahwa untuk y = u – v maka y' = u' – v'.
Contoh Soal 12 :
Tentukan turunan fungsi berikut.
a. f (x) = x3 – 3x2
b. f(x) = 3x + 
c. f(x) = sin x + cos x
Jawaban :
a. f(x) = x3 – 3x2 maka f '(x) = 3x2 – 6x
b. f(x) = 3x +  = 3x + x–1 maka f '(x) = 3 – x–2= 3 –
= 3x + x–1 maka f '(x) = 3 – x–2= 3 – 
Contoh Soal 13 : Soal UMPTN 1997
Diketahui :
f(x) = 3x2 – 5x + 2
g(x) = x2 + 3x – 3
Jika h(x) = f(x) – 2g(x) maka h’ (x) adalah....
Penyelesaian :
h(x)= f(x) – 2g(x)
= 3x2 – 5x + 2 – 2 (x2 + 3x – 3)
= x2 – 11x + 8
h’(x) = 2x – 11
4. Turunan Fungsi y = c . u
Diketahui, fungsi y = f(x) dengan f(x) = c . u(x), dalam hal ini c konstanta dan u(x) fungsi yang sanggup diturunkan di x = a untuk a bilangan real sehingga :
Misalkan, a ialah sebarang bilangan real sehingga untuk y = f(a) = c . u(a) berlaku f '(a) = c . u'(a). Akibatnya, dari y = cu berlaku y' = c . u'.
Contoh Soal 14 :
Tentukan turunan fungsi berikut.
a. f(x) = 3x2
b. f(x) = 
c. f(x) = 3 cos x
d. f(x) = 
Jawaban :
a. f(x) = 3x2 maka f '(x) = 6x
b. f(x) =  = –8x–1 maka f '(x) = 8x –2 =
= –8x–1 maka f '(x) = 8x –2 = 
c. f(x) = 3 cos x maka f ‘(x) = –3 sin x
d.
5. Turunan Fungsi y = uv
Diketahui, fungsi y = f(x) dengan f(x) = u(x) · v(x), dengan u(x) dan v(x) ialah fungsi yang sanggup diturunkan di x = a, untuk a bilangan real. Oleh sebab itu :
Oleh sebab itu, bila y = f(x) = u(x) · v(x) dengan a bilangan real sebarang berlaku f '(a) = u(a) · v'(a) + v(a) · u'(a). Untuk y = u · v, maka y' = uv' + vu'.
Contoh Soal 15 :
Tentukan turunan fungsi berikut.
a. f(x) = (5x2 – 1) (3x – 2)
b. f(x) = cos x sin x
Pembahasan :
a. f(x) = (5x2 – 1) (3x – 2)
Misalkan, u = 5x2 – 1 maka u' = 10x dan v = 3x – 2 maka v' = 3 sehingga
f '(x) = u (x) . v' (x) + v (x) . u' (x) = (5x2 – 1) . 3 + (3x – 2) . 10x
= 30x2 – 20x + 15x2 – 3 = 45x2 – 20x – 3
b. f(x) = sin x cos x
Misalkan, u(x) = sin x maka u'(x) = cos x dan v(x) = cos x maka v'(x) = -sin x
sehingga f '(x)= u (x) . v' (x) + v (x) . u' (x)
= sin x (– sin x) + cos x . cos x
= cos2 x – sin2 x = cos2 x – (1 – cos2 x)
= 2 cos2 x – 1 = cos 2x
Contoh Soal 16 : Soal UMPTN 1999
Turunan dari y = (1 – x)2(2x + 3) ialah ....
Jawaban :
Misalkan, u = (1 – x)2 maka
u ‘ = 2(1 – x)(–1) = –2(1 – x).
Misalkan, v = (2x + 3) → v ‘ = 2
y = uv
y ‘= u’v + uv’
= –2(1 – x)(2x + 3) + (1 – x)2(2)
= 2(1 – x)[(–2x – 3) + (1 – x)]
= 2(1 – x)(–3x – 2)
= 2(1 – x)(–1)(3x + 2)
= 2(x – 1)(3x + 2).
6. Turunan Fungsi y = un
Diketahui y = f(u) dengan f(u) = un dan u = g(x). Jika fungsi u = g(x) sanggup diturunkan di x = a, untuk a bilangan real maka :
Oleh sebab a bilangan real sebarang maka :
Dengan cara yang sama, dapatkah Anda memperoleh :
Untuk Δx mendekati nol maka Δu mendekati nol sehingga :
f(u) = un, f '(u) =nun – 1 sehingga y'(x) = nun – 1 u'(x).
Untuk y = un , maka y' = nun – 1 u'(x).
Contoh Soal 17 :
Tentukan turunan fungsi berikut.
a. f(x) = (2 + 3x2)9
b. f(x) = (5 + 2x)3 + 
c. c. f(x) = 3 sin3  2 cos2
2 cos2 
Jawaban :
a. f(x) = (2 + 3x2)9
Misalkan, u = 2 + 3x2 maka u’(x) = 6x sehingga f (x)= u9
f ‘(x) = 9u8 . u’(x) = 9(2 + 3x2)8 .6x = 54x(2 + 3x2)8
b. f(x) = (5 + 2x)3 +  = (5 + 2x)3 + (2x + 1)1/2
= (5 + 2x)3 + (2x + 1)1/2
f '(x) = 3(5 + 2x)2 · 2 +  (2x + 1)1/2 . 2 = 6(5 + 2x)2 +
(2x + 1)1/2 . 2 = 6(5 + 2x)2 + 
c. =3%5Cleft+(+3sin%5E%7B2%7D%5Cfrac%7B1%7D%7Bx%7D+%5Cright+)%5Cleft+(+cos%5Cfrac%7B1%7D%7Bx%7D+%5Cright+)%5Cleft+(+-%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D+%5Cright+)+2%5Cleft+(+2cos%5Cfrac%7Bx%7D%7B2%7D+%5Cright+)%5Cleft+(+%5Cfrac%7B1%7D%7B2%7D+%5Cright+))
7. Aturan Rantai
Perhatikan kembali uraian materi wacana fungsi y = un. Dari uraian tersebut, diperoleh bahwa untuk y = f(u) = un dengan u = g(x) maka turunannya y' = nun – 1 u'(x). Hasil tersebut menggambarkan hukum rantai.
Misalkan, y = f(u) dan u = g(x).
(f o g)(x) = f{g(x)} = f(u) = y
Jika fungsi g mempunyai turunan di x dan fungsi f mempunyai turunan di u, turunan fungsi komposisi y = f{g(x)} = f o g(x) ditentukan sebagai berikut. (f o g)'(x) = f '(g(x)) . g'(x)
atau 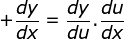
Contoh Soal 18 :
Tentukan turunan fungsi y = %5E%7B6%7D)
Pembahasan :
Misalkan, u = %5E%7B6%7D) maka y = u6.
maka y = u6.
8. Turunan Fungsi y = u/v
Diketahui, fungsi y = f(x) dengan f(x) = %7D%7Bv%5Cleft+(+x+%5Cright+)%7D) , dalam hal ini u(x) dan v(x) fungsi yang sanggup diturunkan di x = a untuk a bilangan real maka :
, dalam hal ini u(x) dan v(x) fungsi yang sanggup diturunkan di x = a untuk a bilangan real maka :
Oleh sebab itu, bila y = f(x) = %7D%7Bv%5Cleft+(+x+%5Cright+)%7D) dengan a sebarang bilangan
dengan a sebarang bilangan
real sehingga berlaku f '(a) = .v%5Cleft+(+a+%5Cright+)-v%5Cleft+(+a+%5Cright+).v%5C,+'%5Cleft+(+a+%5Cright+)%7D%7B%5Cleft+(+v%5Cleft+(+a+%5Cright+)+%5Cright+)%5E%7B2%7D%7D)
maka f '(x) = .v%5Cleft+(+a+%5Cright+)-v%5Cleft+(+a+%5Cright+).v%5C,+'%5Cleft+(+a+%5Cright+)%7D%7B%5Cleft+(+v%5Cleft+(+a+%5Cright+)+%5Cright+)%5E%7B2%7D%7D)
Untuk y = u/v , berlaku y' = 
Contoh Soal 19 :
Tentukan turunan fungsi berikut.
a. f(x) = cosec x
b. f(x) = tan x
Pembahasan :
a. f(x) = cosec x = 
Misalkan u = 1 maka u' = 0 dan v = sin x maka v' = cos x.
f '(x) = sec2 x.
Contoh Soal 20 :
Tentukan turunan fungsi berikut.
a. f(x) = 
b. f(x) = %5E%7B3%7D%5Cleft+(+2x+3+%5Cright+)%7D%7B2x%5E%7B2%7D%7D)
Pembahasan :
a. Misalkan, u = x – 2 maka u' = 1 dan v = x + 2 maka v' = 1.
b. f(x) =%5E%7B3%7D%5Cleft+(+2x+3+%5Cright+)%7D%7B2x%5E%7B2%7D%7D)
Misalkan, u = (x – 1)3(2x + 3) maka u’ = 3(x – 1)2(2x + 3) + (x –1)3(2) v = 2x2 maka v’= –4x.
Contoh Soal 21 (Soal UMPTN 1997) :
a. Misalkan, u = x – 2 maka u' = 1 dan v = x + 2 maka v' = 1.
b. f(x) =
Misalkan, u = (x – 1)3(2x + 3) maka u’ = 3(x – 1)2(2x + 3) + (x –1)3(2) v = 2x2 maka v’= –4x.
Contoh Soal 21 (Soal UMPTN 1997) :
Jika f(x) =  , maka turunan f –1(x) ialah ....
, maka turunan f –1(x) ialah ....
Kunci Jawaban :
Contoh Soal 22 :
Sebuah peluru ditembakkan vertikal ke atas dengan kecepatan awal 10 m/detik. Kedudukan peluru sehabis t detik memenuhi persamaan h(t) = 30t – 6t² dengan h(t) ialah tinggi peluru yang diukur dalam meter.
a. Carilah kecepatan peluru pada ketika 1,5 detik.
b. Kapan peluru berhenti?
Jawaban :
Diketahui:
Kecepatan awal peluru = 10 m/detik.
Kedudukan peluru pada t detik = h(t) = 30t – 6t².
Ditanyakan:
a. Kecepatan peluru pada ketika 1,5 detik.
b. Kapan peluru berhenti.
Penyelesaian :
a. Dalam fisika, kecepatan merupakan turunan dari kedudukan terhadap waktu sehingga v(t) = h'(t) = 30 – 12t. Jadi, kecepatan peluru pada ketika t = 1,5 ialah :
v(1,5) = 30 –12(1,5) = 12 m/detik.
b. Peluru akan berhenti ketika kecepatannya nol sehingga v(t ) = 0
↔ 30 – 12t = 0
↔ t = 2,5.
Jadi, peluru berhenti pada ketika 2,5 detik.
C. Persamaan Garis Singgung pada Kurva
Telah Anda ketahui bahwa kemiringan (gradien) garis singgung kurva y = f(x) di titik A(a, f(a)) ialah :
Persamaan garis lurus yang melalui titik P(x1, y1) dengan gradien m ialah :
y – y1 = m(x – x1)
Dengan demikian, persamaan garis singgung g di titik A(a, f(a)) pada kurva ialah :
y – f(a) = f '(a) (x – a)
Contoh Soal 23 :
Tentukan persamaan garis singgung pada kurva berikut.
a. f(x) = x2 di titik (–2, 4)
b. y = x3 di titik yang mempunyai absis x = 1 dan x = 2.
Jawaban :
a. Persamaan garis singgung pada kurva f(x) = x2 di titik (–2, 4) ialah y – 4 = f '(–2) (x – (–2)).
f(x) = x2 maka f '(x) = 2x sehingga f '(–2) = 2(–2) = –4
Jadi, persamaan garis singgung pada kurva f(x) = x2 di titik (–2, 4) ialah y – 4 = –4 (x + 2) ↔ y = –4 x – 4.
b. Untuk absis x = 1.
Persamaan garis singgung pada kurva f(x) = x3 adalah :
y – f (1) = f '(1) (x – 1)
f(1) dan f '(1) ditentukan sebagai berikut: f(x) = x3 maka :
f(1) = 13 = 1.
f '(x) = 3x2 sehingga f '(1) = 3 . 12 = 3
Jadi, persamaan garis singgung pada kurva f(x) = x3 di titik (1, 1) ialah y – 1 = 3 (x – 1) ↔ y = 3x – 2.
Untuk absis x = 2.
Persamaan garis singgung pada kurva f(x) = x3 adalah :
y – f(2) = f '(2) (x – 2)
f(2) dan f '(2) ditentukan sebagai berikut: f(x) = x3 maka :
f(2) = 23 = 8.
f '(x) = 3x2 sehingga f '(2) = 3 . 22 = 12
Jadi, persamaan garis singgung pada kurva f(x) = x3 di titik (2,8) ialah y – 8 = 12(x – 2) ↔ y = 12x – 16.
Menentukan Persamaan Garis Singgung pada Kurva bila Gradien Garis Singgung Diketahui
Untuk memilih persamaan garis singgung pada kurva apabila gradien garis singgung diketahui, pelajari beberapa tumpuan berikut.
Untuk memilih persamaan garis singgung pada kurva apabila gradien garis singgung diketahui, pelajari beberapa tumpuan berikut.
Contoh Soal 24 :
Tentukan persamaan garis singgung pada kurva berikut.
a. y = f(x) di titik (1, 4) bila f '(x) = 3x2 + 6x
b. y=f(x) dengan f(x) = 2x3 yang tegak lurus terhadap garis y = 
Pembahasan :
a. Persamaan garis singgung pada kurva y = f (x) di titik (1, 4), berdasarkan rumus ialah y – f (1) = f '(1) (x – 1). Diketahui f(1) = 4 dan f '(x) = 3x2 + 6x maka :
f '(1) = 3 . 12 + 6 . 1 = 9.
Jadi, persamaan garis singgung di titik (1, 4) ialah y – 4 = 9 (x – 1) ↔ y = 9x – 5.
b. Jika g: y = mx + n ialah garis singgung pada kurva y = 2x3 dan tegak lurus terhadap garis h: y =
↔ m = 24.
Persamaan garis singgung pada kurva y = 2x3 adalah y – f(x1) = f '(x1) (x – x1 dengan x1 absis titik singgung pada kurva y = 2x3 .
Selanjutnya, nilai x1 ditentukan sebagai berikut.
f '(x) = 6x2 maka f '(x1) = 6x12.
Diketahui f '(x1) = 24 sehingga 6x12 = 24 ↔ x1
2 = 4 ↔ x1 = ± 2.
Untuk x1 = 2, diperoleh f (x1) = 2 . 23 = 16. Persamaan garis
singgung yang tegak lurus terhadap garis y =  adalah :
adalah :
y – 16 = 24 (x – 2) ↔ y = 24x – 32.
Coba Anda tentukan persamaan garis singgung untuk x1 = –2.
Contoh Soal 25 Soal UMPTN 2001 :
Kurva y = (x2 + 2)2 memotong sumbu-y di titik A. Persamaan garis singgung pada kurva tersebut di A ....
Penyelesaian :
A ialah titik potong kurva y = (x2 + 2)2 terhadap sumbu-y.
absis xA = 0
yA = (0 + 2)2 = 4
m =  = 2(2x)(x2 + 2)
= 2(2x)(x2 + 2)
mA = 2(0)(0 +2) = 0
Persamaan garis singgung :
y – yA = mA(x – xA)
y – 4 = 0 ↔ y = 4
D. Turunan Kedua
Anda telah mempelajari turunan pertama fungsi yang dinotasikan dengan :
 atau y' atau
atau y' atau  atau f '(x)
atau f '(x)
Fungsi turunan dari turunan pertama dinamakan fungsi turunan kedua yang dinotasikan dengan :
=%5Cfrac%7Bd%5E%7B2%7Dy%7D%7Bdx%5E%7B2%7D%7D) atau ditulis y"
atau ditulis y"
=%5Cfrac%7Bd%5E%7B2%7Df%7D%7Bdx%5E%7B2%7D%7D) atau ditulis f "(x)
atau ditulis f "(x)
Turunan kedua fungsi f(x)
 atau y" atau
atau y" atau  atau f "(x)
atau f "(x)
Contoh Soal Turunan Kedua 26 :
Tentukan turunan kedua untuk fungsi berikut.
a. f(x) = 2x4 – 5x
b. f(x) = x sin x
Pembahasan :
Turunan kedua fungsi f(x) = 2x4 – 5x ialah f''(x) = 24x2.
b. f(x) = sin x
sin x
f '(x) = sin x +
sin x +  cos x =
cos x =  sin x +
sin x +  cos x
cos x
f "(x) = - sin x +
sin x +  cos x =
cos x =  cos x -
cos x -  sin x
sin x
f "(x) = - sin x +
sin x +  cos x -
cos x -  sin x
sin x
Turunan kedua dari f(x) = sin x ialah :
sin x ialah :
f "(x) = - sin x +
sin x +  cos x -
cos x -  sin x
sin x
Contoh Soal 27 :
Sebuah benda yang bergerak lurus pada lintasan (s) memenuhi persamaan t3 – 6t2 + 30t. Dalam hal ini, s dalam meter dan t dalam detik.
a. Hitunglah panjang lintasan pada ketika t = 3 dan t = 5.
b. Tentukan kecepatan dan percepatan benda sehabis t = 4 detik.
c. Hitunglah laju pada waktu percepatannya nol.
Jawaban :
a. Pada ketika t=3, panjang lintasannya ialah :
Pada ketika t = 5, panjang lintasannya adalah
Kecepatan v = = 3t2 – 12t + 30
= 3t2 – 12t + 30
Kecepatan pada t = 4 sekon adalah v(4) = 3.42 – 12.4 + 30 = 30 m/detik
Pecepatan a = =
=  = 6t – 12
= 6t – 12
Percepatan pada t = 4 sekon adalah a(4) = 6.4 – 12 = 12 m/detik2
c. a = 0 maka 6t – 12 = 0 ↔ t = 2
v(t) = 3t2 – 12t + 30, untuk t = 2 maka v(2) = 3.22 – 12.2 + 30 = 18 m/detik
E. Teorema L’ Hopital
Jika x = a disubstitusikan ke bentuk%7D%7Bg%5Cleft+(+x+%5Cright+)%7D) diperoleh bentuk tak tentu
diperoleh bentuk tak tentu  atau
atau  , Anda sanggup memakai teorema L' Hopital. Teorema ini dikemukakan kali pertama oleh Marquis L' Hopital, seorang matematikawan Prancis (1661–1704 M).
, Anda sanggup memakai teorema L' Hopital. Teorema ini dikemukakan kali pertama oleh Marquis L' Hopital, seorang matematikawan Prancis (1661–1704 M).
Definisi Soal 28 :
Jika f (x) = 0,
f (x) = 0,  g (x) = 0, serta
g (x) = 0, serta %7D%7Bg%5C,+'%5Cleft+(+x+%5Cright+)%7D) ada, baik terhingga atau tak hingga maka :
ada, baik terhingga atau tak hingga maka :
%7D%7Bg%5Cleft+(+x+%5Cright+)%7D=%5Clim_%7Bx%5Crightarrow+a%7D%5Cfrac%7Bf%5C,+'%5Cleft+(+x+%5Cright+)%7D%7Bg%5C,+'%5Cleft+(+x+%5Cright+)%7D)
Perluasan teorema L'Hopital ialah :
%7D%7Bg%5Cleft+(+x+%5Cright+)%7D=%5Clim_%7Bx%5Crightarrow+a%7D%5Cfrac%7Bf%5C,+'%5Cleft+(+x+%5Cright+)%7D%7Bg%5C,+'%5Cleft+(+x+%5Cright+)%7D%3D%5Clim_%7Bx%5Crightarrow+a%7D%5Cfrac%7Bf%5C,+''%5Cleft+(+x+%5Cright+)%7D%7Bg%5C,+''%5Cleft+(+x+%5Cright+)%7D%3D%5Clim_%7Bx%5Crightarrow+a%7D%5Cfrac%7Bf%5C,+'''%5Cleft+(+x+%5Cright+)%7D%7Bg%5C,+'''%5Cleft+(+x+%5Cright+)%7D)
(Proses berakhir bila hasil tamat tidak berbentuk ).
).
Contoh Soal 29 :
Tentukan limit fungsi berikut.
a.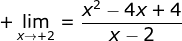
b.
Jawaban :
a. Jika dengan memakai substitusi langsung, diperoleh :
%5E%7B2%7D-4%5Cleft+(+2+%5Cright+)+4%7D%7B2-2%7D%3D%5Cfrac%7B0%7D%7B0%7D) (bentuk tak tentu)
(bentuk tak tentu)
Dengan teorema L' Hopital, diperoleh :
%5E%7B2%7D-4%5Cleft+(+2+%5Cright+)+4%7D%7B1%7D%3D2%5Cleft+(+2+%5Cright+)-4%3D0)
b. Jika memakai substitusi eksklusif diperoleh :
Anda kini sudah mengetahui Turunan Fungsi. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.
Anda telah mempelajari turunan pertama fungsi yang dinotasikan dengan :
Fungsi turunan dari turunan pertama dinamakan fungsi turunan kedua yang dinotasikan dengan :
Turunan kedua fungsi f(x)
Contoh Soal Turunan Kedua 26 :
Tentukan turunan kedua untuk fungsi berikut.
a. f(x) = 2x4 – 5x
b. f(x) = x sin x
Pembahasan :
a. f(x) = 2x4 – 5x
f ‘(x) = 8x3 – 5
f “(x) = 24x2Turunan kedua fungsi f(x) = 2x4 – 5x ialah f''(x) = 24x2.
b. f(x) =
f '(x) =
f "(x) = -
f "(x) = -
Turunan kedua dari f(x) =
f "(x) = -
Contoh Soal 27 :
Sebuah benda yang bergerak lurus pada lintasan (s) memenuhi persamaan t3 – 6t2 + 30t. Dalam hal ini, s dalam meter dan t dalam detik.
a. Hitunglah panjang lintasan pada ketika t = 3 dan t = 5.
b. Tentukan kecepatan dan percepatan benda sehabis t = 4 detik.
c. Hitunglah laju pada waktu percepatannya nol.
Jawaban :
a. Pada ketika t=3, panjang lintasannya ialah :
s(3) = 33 – 6.32 + 30.3 = 63 meter
Pada ketika t = 5, panjang lintasannya adalah
s(5) = 53 – 6.52 + 30.5 =125 meter
b. s = t3 – 6t2 + 30t
Kecepatan v =
Kecepatan pada t = 4 sekon adalah v(4) = 3.42 – 12.4 + 30 = 30 m/detik
Pecepatan a =
Percepatan pada t = 4 sekon adalah a(4) = 6.4 – 12 = 12 m/detik2
c. a = 0 maka 6t – 12 = 0 ↔ t = 2
v(t) = 3t2 – 12t + 30, untuk t = 2 maka v(2) = 3.22 – 12.2 + 30 = 18 m/detik
E. Teorema L’ Hopital
Jika x = a disubstitusikan ke bentuk
Definisi Soal 28 :
Jika
Perluasan teorema L'Hopital ialah :
(Proses berakhir bila hasil tamat tidak berbentuk
Contoh Soal 29 :
Tentukan limit fungsi berikut.
a.
b.
Jawaban :
a. Jika dengan memakai substitusi langsung, diperoleh :
Dengan teorema L' Hopital, diperoleh :
b. Jika memakai substitusi eksklusif diperoleh :
Anda kini sudah mengetahui Turunan Fungsi. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.


































No comments:
Post a Comment