Pintar Pelajaran Rumus Rujukan Soal Permutasi Dan Kombinasi, Pengertian, Unsur Yang Sama, Siklis, Cara Menentukan, Binomial Newton, Peluang, Jawaban, Matematika

Rumus Contoh Soal Permutasi dan Kombinasi, Pengertian, Unsur yang Sama, Siklis, Cara Menentukan, Binomial Newton, Peluang, Jawaban, Matematika - Berikut ini yakni bahan lengkap permutasi dan kombinasi :

3. Permutasi

Dalam suatu kelas,terdapat 4 orang yang akan dipilih 3 orang untuk menjadi ketua, sekretaris, dan bendahara. Banyak cara untuk menentukan 3 orang tersebut sanggup dijelaskan sebagai berikut. Misal, keempat orang kandidat itu yakni A, B, C, dan D. Posisi ketua sanggup dipilih dengan 4 cara, posisi sekretaris sanggup dipilih dengan 3 cara, dan posisi bendahara sanggup dipilih dengan 2 cara. Makara banyak cara yang dilakukan untuk menentukan 3 orang pengurus kelas dari 4 orang kandidat yakni 4 × 3 × 2 = 24 cara. Uraian tersebut akan lebih terperinci apabila Anda mengamati sketsa berikut.

Gambar 1. Diagram pohon untuk pemilihan 3 pengurus kelas dari 5 calon yang ada.

Ingatlah :

Urutan ABC C berbeda dengan urutan ACB. Dalam urutan ABC, sekretaris yakni B. Dalam urutan ACB, sekretaris yakni C.

Dari sketsa tersebut diperoleh 24 susunan 3 unsur, yaitu :

ABC	ABD	ACB	ACD	ADB	ADC
BAC	BAD	BCA	BCD	BDA	BCD
CAB	CAD	CBA	CBD	CDA	CDB
DAB	DAC	DBA	DBC	DCA	DCB

Tampak susunan 3 unsur tersebut memperhatikan urutannya. ABC yakni suatu permutasi, ACB juga suatu permutasi dan keduanya berbeda. Urutan pada 24 susunan itu berlainan. Susunan yang memperhatikan urutannya disebut permutasi. Dari uraian tersebut dapatkah Anda menduga pengertian permutasi? Cobalah nyatakan pengertian permutasi dengan kata-kata Anda sendiri. Konsep yang telah Anda pelajari tersebut memperjelas definisi berikut.

Definisi 1 :

Permutasi yakni urutan yang mungkin dari sejumlah unsur yang berbeda tanpa adanya pengulangan.

Banyaknya permutasi 3 unsur yang diambil dari 4 unsur yakni :

4 × 3 × 2 = 24.

Banyaknya permutasi 3 unsur yang diambil dari 4 unsur sanggup ditulis :

Permutasi r unsur yang diambil dari n unsur sanggup dipelajari melalui Tabel 1.

Tabel 1. Permutasi r unsur yang diambil dari n unsur

Tempat ke-	1	2	3	...	r	...
Banyak Cara	n	n(n – 1)	n(n – 1) (n – 2)	...	n(n – 1) (n – 2)...(n – (r – 1))	...

Dari tabel tersebut, banyak permutasi r unsur yang diambil dari n unsur, dinotasikan P(n, r) yakni :

P(n, r) = n (n – 1) (n – 2) … (n – (r – 1))

Untuk r = 1, maka :

P(n, 1) = n

Untuk r = 2, maka P(n, 2) :

Ingatlah :

Notasi P(n, k) sanggup juga ditulis dengan  .

Untuk r = 3 maka P(n, 3) :

Untuk r = k, diperoleh P(n, k) :

Untuk r = n, diperoleh :

P(n, n) = n (n – 1)(n – 2)…(n – (r – 1))(n – r)…(3)(2)(1) = n!

Banyak permutasi n unsur apabila disusun dalam k unsur yakni :

Contoh Soal 1

Tiga orang wiraniaga dicalonkan untuk mengisi kekosongan jabatan kepala cabang di dua kota. Tentukan banyak cara untuk menentukan dua kepala cabang dari tiga orang wiraniaga tersebut, dengan memakai rumus permutasi.

Jawaban 1

P(3, 2), dengan n = 3 (banyak wiraniaga) dan k = 2 (banyak wiraniaga terpilih).

Jadi, terdapat 6 cara.

Coba Anda tentukan ke-6 susunan yang mungkin tersebut.

Contoh Soal 2

Dari kartu angka 4, 5, 6, 7, dan 8 dibentuk bilangan yang terdiri atas tiga angka yang berbeda. Tentukan banyaknya bilanganbilangan tersebut yang kurang

a. dari 500 b. dari 600

Penyelesaian 2

a. Oleh sebab bilangan-bilangan kurang dari 500 maka angka ratusan hanya sanggup diisi oleh satu angka, yaitu angka 4. Salah satu susunan yang mungkin sanggup Anda lihat pada Gambar 2. Amati gambar 3.

Gambar 2. Salah satu susunan yang mungkin. Dapatkah Anda menentukan susunan lainnya?

Angka puluhan dan satuan sanggup diisi oleh angka 5, 6, 7, dan 8. Ini berarti Anda harus menentukan dua angka dari 4 angka, yaitu :

Jadi, terdapat 12 cara untuk menyusun bilangan kurang dari 500. Dapatkah Anda mengerjakan dengan cara lain? Silakan coba.

Gambar 3. Angka puluhan dan satuan sanggup diisi oleh angka 5, 6, 7, dan 8.

Sekarang, coba Anda buktikan hal ini dengan memakai kartu angka. Tentukan pula susunan-susunan yang mungkin.

b. Oleh sebab bilangan-bilangan itu kurang dari 600 maka angka ratusan hanya diisi oleh dua angka, yaitu angka 4 dan 5.

4 → angka puluhan dan satuan sanggup diisi oleh angka 5, 6, 7, dan 8 (pilih 2 dari 4 unsur).

5 → angka puluhan dan satuan sanggup diisi oleh angka 4, 6, 7, dan 8 (pilih 2 dari 4 unsur).

Banyak bilangan yang kurang dari 600 yakni :

Jadi, terdapat 24 bilangan yang kurang dari 600.

3.1. Permutasi Beberapa Unsur yang Sama

Pada kata "BUKU" terdapat dua karakter yang sama, yaitu U. Permutasi huruf-huruf pada kata "BUKU" sanggup Anda amati pada diagram pohon di bawah.

Coba Anda buat diagram pohon untuk huruf-huruf: U, K, dan U. Jika benar mengerjakannya, hasil dari seluruh diagram pohon tersebut yakni sebagai berikut.

1. BUKU	6. BUUK	11. UBUK	16. KBUU	21. UUBK
2. BUUK	7. UKBU	12. UBKU	17. KUUB	22. UUKB
3. BKUU	8. UKUB	13. KUBU	18. KUBU	23. UKBU
4. BKUU	9. UUBK	14. KUUB	19. UBUK	24. UKUB
5. BUKU	10. UUKB	15. KBUU	20. UBKU

Amatilah 24 susunan karakter tersebut. Tampak ada beberapa susunan karakter yang sama sehingga permutasinya menjadi:

1. BUKU	4. UKBU	7. UUKB	10. KUBU
2. BUUK	5. UKUB	8. UBUK	11. KUUB
3. BKUU	6. UUBK	9. UBKU	12. KBUU

Banyak permutasi huruf-huruf pada kata “BUKU” yakni 12 atau 12 = 4 × 3 = (4 x 3 x 2 x 1) / (2 x 1) = 4!/2!

Sekarang, selidikilah permutasi untuk kata MAMA dengan memakai diagram pohon. Jika Anda melaksanakan dengan benar, terdapat 6 permutasi yang berbeda, yaitu MAMA, MAAM, MMAA, AMMA, AMAM, dan AAMM, sebab kata “MAMA” memiliki dua pasang karakter yang sama.

Banyak permutasi untuk 4 unsur dengan dua pasang unsur sama, yaitu M dan dua unsur lainnya, yaitu A yakni :

Banyaknya permutasi n unsur yang mempunyai l₁ unsur jenis pertama, l₂ unsur jenis kedua, l₃ unsur jenis ketiga, dan l_k unsur jenis ke-k yang sama yakni :

Contoh Soal 3

Tentukan permutasi atas semua unsur yang sanggup dibentuk dari kata-kata berikut.

a. JAYAPURA 

b. MATEMATIKA

Pembahasan 3

a. Pada kata "JAYAPURA", terdapat 3 buah A yang sama sehingga permutasinya yakni P(8, 3) = 8! / 3! = 6.720.

b. Pada kata "MATEMATIKA" terdapat 2 buah M, 3 buah A, dan 2 buah T yang sama sehingga permutasinya yakni :

3.2. Permutasi Siklis

Permutasi yang dibentuk dengan menyusun unsur secara melingkar berdasarkan arah putaran tertentu disebut permutasi siklis.

Gambar 4. Permutasi Siklis

Pada Gambar 4. posisi 1 dan posisi 2 menawarkan permutasi A dan B yang disusun melingkar searah putaran jarum jam. Coba Anda amati Gambar 4, apakah susunan pada posisi 1 berbeda dengan susunan pada posisi 2? Apabila Anda mengamati dengan saksama maka posisi 1 = posisi 2

Jadi, permutasi siklis dua unsur memiliki satu cara.

Pada permutasi siklis dua unsur, satu unsur ditetapkan sebagai titik acuan. Sementara, satu unsur yang lainnya ditempatkan dalam 1! cara atau (2 – 1)! cara. Agar Anda lebih memahami permutasi siklis, pelajari uraian berikut ini. Misalkan, dalam satu ruangan ada 4 orang masing-masing diberi nama A, B, C, dan D. Keempat orang tersebut sedang membaca di meja bundar. Banyak cara keempat orang itu duduk melingkari meja bulat sanggup diterangkan sebagai berikut.

Gambar 5. Banyak cara keempat orang itu duduk melingkari meja bundar.

Dengan cara yang sama, Anda sanggup menciptakan deretan lingkaran untuk titik pangkal B, C, dan D. Hasil dari seluruh deretan lingkaran tersebut yakni sebagai berikut.

1. ABCD	7. BACD	13. CABD	19. DABC
2. ABDC	8. BADC	14. CADB	20. DACB
3. ACBD	9. BCAD	15. CBAD	21. DBAC
4. ACDB	10. BCDA	16. CBDA	22. DBCA
5. ADBC	11. BDAC	17. CDAB	23. DCAB
6. ADCB	12. BDCA	18. CDBA	24. DCBA

Amati bahwa ada susunan-susunan yang sama, yaitu :

ABCD = BCDA= = CDAB = DABC	ACDB = BACD = CDBA = DBAC
ABDC = BDCA= = CABD= = DCAB	ADBC = BCAD= = CADB= = DBCA
ACBD = BDAC = CBDA = DACB	ADCB = BADC = CBAD = DCBA

Dengan demikian, dari 24 susunan tersebut terdapat 6 susunan yang berbeda, yaitu ABCD, ABDC, ACBD, ACDB, ADBC, dan ADCB. Jadi, banyak permutasi siklis dari 4 unsur ada 6.

Pada permutasi siklis dari 4 unsur, ditetapkan satu unsur sebagai titik pangkal, kemudian 3 unsur lainnya ditempatkan dalam 3! cara atau (4 – 1)! cara. Permutasi siklis 4 unsur yakni (4 – 1)! = 3! = 3 × 2 × 1 = 6 cara.

Susunan manik-manik pada kalung ibarat susunan melingkar, tetapi berbeda dengan permutasi siklis. Pada permutasi siklis, arah putaran diperhatikan, sedangkan pada susunan manik-manik dalam kalung arah putaran tidak diperhatikan. Amati Gambar 6.

Gambar 6. Contoh permutasi siklis.

Dari gambar, susunan manik-manik pada posisi 1 yakni ABC atau ditulis ACB. Adapun susunan manik-manik pada posisi 2 yakni ACB atau ditulis ABC.

Gambar 7. susunan manik-manik pada posisi 2 yakni ACB atau ditulis ABC.

Susunan manik-manik pada Gambar 7. yakni sama. Oleh sebab itu, banyak cara menyusun 3 manik-manik dalam kalung yakni 1 susunan. Banyaknya cara yang dipakai untuk menyusun 3 manik-manik dalam kalung yakni setengah dari banyak permutasi siklis 3 unsur, yaitu 1 susunan atau (3-1)!/2.

Untuk n unsur, apabila disusun ibarat manik-manik dalam kalung terdapat (n-1)!/2 susunan yang berbeda.

Ingatlah :

Gambar 9. Susunan pada gambar (a) dan gambar (b) yakni sama sebab unsur A bersahabat dengan D dan B, meskipun titik contoh berbeda.

Contoh Soal 4

a. Delapan orang ilmuwan duduk melingkar di sebuah meja bulat untuk membahas sebuah proyek tertentu. Berapa banyak cara supaya para ilmuwan sanggup duduk melingkar dengan urutan yang berbeda?

b. Dua puluh lima mutiara akan dibentuk sebuah kalung. Ada berapa cara mutiara-mutiara itu sanggup disusun?

Pembahasan 4

a. Susunan kedelapan ilmuwan itu yakni (8–1)! = 7! = 5.040 cara.

b. Banyaknya cara mutiara itu sanggup disusun menjadi sebuah kalung yakni :

(25-1) / 2 = 24!/2 cara

4. Kombinasi

Pada permutasi, Anda telah sanggup menentukan 3 orang dari 5 orang untuk menjadi ketua, sekretaris, dan bendahara. Lain halnya jikalau dari 5 orang itu akan dipilih 3 orang untuk mengikuti lomba debat. Banyak cara untuk menentukan 3 orang tersebut tidak sebanyak 60 cara ibarat pada pemilihan ketua, sekretaris, dan bendahara. Agar lebih jelasnya, pelajari uraian berikut.

Misalkan, dari 5 orang akan dipilih 3 orang untuk mengikuti lomba debat. Banyak cara untuk menentukan 3 orang tersebut sanggup diterangkan sebagai berikut.

Dari Subbab A.3 telah dijelaskan bahwa susunan 3 unsur dari 5 unsur, yaitu :

ABC	ADE	BCD	CAB	CDE	DBC	EAB	ECD
ABD	AEB	BCE	CAD	CEA	DBE	EAC	EDA
ABE	AEC	BDA	CAE	CEB	DCA	EAD	EDB
ACB	AED	BDC	CBA	CED	DCB	EBA	EDC
ACD	BAC	BDE	CBD	DAB	DCE	EBC
ACE	BAD	BEA	CBE	DAC	DEA	EBD
ADB	BAE	BEC	CDA	DAE	DEB	ECA
ADC	BCA	BED	CDB	DBA	DEC	ECB

Oleh sebab pemilihan 3 orang untuk mengikuti lomba debat tidak memperhatikan urutan maka dari 60 susunan itu terdapat 10 susunan yang berbeda. Kesepuluh susunan tersebut yakni ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, dan CDE.

Susunan yang tidak memperhatikan urutannya disebut kombinasi.

Dari uraian tersebut, dapatkah Anda menyatakan pengertian kombinasi? Cobalah nyatakan pengertian kombinasi dengan kata-kata Anda sendiri. Konsep pengertian kombinasi yang telah Anda pelajari tersebut memperjelas definisi berikut.

Definisi 3 :

Kombinasi r unsur dari n unsur yakni himpunan potongan r unsur yang sanggup diambil dari n unsur yang berlainan dengan urutan penyusunan unsur tidak diperhatikan.

Banyaknya dengan  atau  atau C =(n, r).

4.1. Menentukan Banyak Kombinasi 

Telah diketahui bahwa banyaknya kombinasi 5 unsur berlainan jikalau disusun sebanyak 3 unsur yakni (5 x 4) / 2 = 10 cara.

Kombinasi 5 unsur yang disusun atas 3 unsur ditulis :

Uraian tersebut memberi citra mengenai banyaknya kombinasi n unsur berlainan jikalau disusun sebanyak r unsur yang dirumuskan :

 dengan r < n

Contoh Soal 5

Kerjakan soal-soal berikut.

a. Diketahui 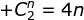, tentukanlah nilai n.

b. Dari 20 siswa akan dipilih sebuah tim sepakbola yang terdiri atas 11 orang. Tentukan banyak cara dalam pemilihan tersebut.

Pembahasan 5

1.

Oleh sebab n ≥ r maka yang memenuhi yakni n = 9.

b. Pemilihan tim sepakbola tersebut yakni problem kombinasi sebab tidak memperhatikan urutan. Banyak cara menentukan 11 orang siswa dari 20 siswa, yaitu .

Coba Anda tentukan susunannya dengan diagram pohon.

Contoh Soal 7 : Soal Ebtanas 2000

Suatu pertemuan dihadiri oleh 15 orang undangan. Jika mereka saling berjabat tangan, banyak jabat tangan yang terjadi dalam pertemuan itu yakni ....

Jawaban 7

Banyak jabat tangan = C(15,2)

15!/(2!13!) = 105

Contoh Soal : Soal UMPTN 2000 

Banyaknya segitiga yang sanggup dibentuk dari 7 titik tanpa ada tiga titik yang terletak segaris yakni ....

Jawab:

Membuat segitiga dengan menentukan 3 titik dari 7 titik yang tersedia yakni problem kombinasi C(7, 3). Jadi, banyaknya segitiga = C(7,3)

4.2. Binomial Newton

Di Sekolah Menengah Pertama Anda telah mempelajari cara menjabarkan bentuk perpangkatan berikut.

(a + b)⁰ = 1
(a + b)¹ = a + b
(a + b)² = a² + 2ab + b²
 (a + b)³ = a³ + 3a²b + 3ab² + b³

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Untuk pangkat 4, Anda masih sanggup menjabarkannya. Bagaimana menjabarkan (a+b)15? Untuk menyelesaikannya Anda memerlukan rumus umum bentuk perpangkatan tersebut.

Amati dengan saksama koefisien-koefisien bentuk-bentuk perpangkatan tersebut. Apabila koefisien-koefisien dari bentuk perpangkatan dituliskan dalam bentuk diagram, diperoleh :

Diagram itu dikenal dengan nama Segitiga Pascal. Amati pola Segitiga Pascal tersebut.

Karena :

maka pola Segitiga Pascal tersebut sanggup dituliskan dalam bentuk simbol banyaknya kombinasi berikut.

Dari uraian tersebut, bentuk perpangkatan sanggup dituliskan sebagai berikut.

Secara umum bentuk (a + b)ⁿ dapat ditulis menjadi :

dengan :

Dengan demikian,

Bentuk tersebut dinamakan binomial Newton (ekspansi binomial).

Contoh Soal 8

Jabarkan dan sederhanakan bentuk (x² + 2y)⁵.

Penyelesaian 8

Anda kini sudah mengetahui Permutasi dan Kombinasi. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi :

Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.